
Велосипедист проехал с определенной скоростью путь в 10 км от города до турбазы. Возвращаясь обратно, он снизил скорость на 5 км\ч. На весь путь туда и обратно он потратил 1ч 10 мин. Найдите скорость, с которой велосипедист ехал от турбазыдо города.
Пусть скорость велосипедиста -х км/ч
Тогда снизив скорость на 5 км/ч он ехал со скоростью х-5
На весь путь туда и обратно он потратил 1ч 10мин =1+10/60 =1 1/6 часа =7/6 часа
Запишем уравнение
10/x+10/(x-5) = 7/6
(10(x-5)+10x)/(x*(x-5)) =7/6
(20x-50)/(x*(x-5))=7/6
Поскольку х и х-5 не равны нулю
то можно умножить обе части уравнения на х(х-5)
20х-50 =x(x-5)*7/6
120x-300 =7x^2-35x
7x^2-155x+300 =0
D =15625
x1 =(155-125)/14 = 30/14 =15/7 =2 1/7 ( неподходит так как скорость не может быть меньше 5 км/ч)
x2 =(155+125)/7 = 40 км/ч
Бассейн объемом 1м(в кубе) заполняется двумя насосами одновременно. Первый насос перекачивает за 1ч на 1м(в кубе) больше , чем второй. Найдите время, за которое каждый насос в отдельности может наполнить бассейн, если первому насосу нужно для этого на 5 мин меньше, чем второму.
Пусть производительность второго насоса х м^3/час тогда производительность первого насоса x+1
Разница по времени составила 5 мин =5/60 час = 1/12 час
Запишем уравнение
1/x -1/(x+1) =1/12
1/(x*(x+1)) =1/12
Поскольку х х+1 не могут равнятся нулю то можно умножить обе части неравенства на х(х+1)
1 = х(х+1)/12
12 =x^2+x
x^2+x-12 =0
D = 1+24 =25
x1=(-1-5)/2=-3 ( производительность не может быть отрицательной)
х2=(-1+5)/2 =3
Производительность первого насоса
х+1 = 3+1 =4 м^3/ч
Время заполнения басейна 1 насосом
1м^3/4м^3/ч= 1/4 час = 60/4 мин= 15 мин
Время заполнения басейна вторым насосом
1/3 =60/3 мин = 20 мин
y = - 3x + 2 и y = kx - 5 пересекаются, значит мы приравниваем эти функции:
-3x + 2 = kx - 5
kx + 3x = 7
x(k + 3) = 7
1. x₁ = 7, тогда k должно быть -2 (так как 7 · (-2 + 3) = 7 · 1 = 7)
2. k + 3 = 7 ⇒ k = 4, тогда x₂ должно быть 1 (так как 1 · (4 + 3) = 7)
Отсюда:
1. y₁ = -3 · 7 + 2 = -19
2. y₂ = 4 · 1 - 5 = -1 ≠ y₁ следовательно, подставим x и k из первого заключения:
y₂ = -2 · 7 - 5 = -14 - 5 = -19 = y₁
Получится точка A:
A(7; -19)
Найдём, при каком k функция y = kx + 4 проходит с точкой A, подставив значения из точки A(x;y):
y = kx + 4
-19 = k · 7 + 4
7k = -23
k = -23/7
x⁴ + 3x² - 7 = 0,
Делаем замену переменной x² = t, тогда x⁴ = (x²)² = t²,
t ≥ 0.
t² + 3t - 7 = 0,
D = 3² - 4·1·(-7) = 9 + 28 = 37,
1)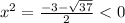
здесь решений нет, т.к. x² ≥ 0.
2)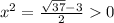
ответ.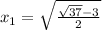
или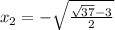 .
.