
Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:
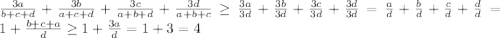
Что и требовалось доказать.
Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.
Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).
Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3
P.S. Если что-то непонятно, то не стесняйся спрашивать)
Единственное решение при любых а, кроме а не=3.
№2. Преобразуем каждое уравнение, т.е. избавимся от знаменателей. В первом уравнении правую часть умножим на 10, а во втором левую часть умножим на 3, а в правой первое и второе слагаемые соответственно умножим на 4 и 3
Тогда получим после перенесения всех неизвестных в левую часть, а чисел в правую
{ 2x+90y=276
4x+9e=39 Поделим обе части первого уравнения на 2, а обе части второго умножим на 5. Получим
{ x+45y=138
20x+45y=195 Вычтем из второго уравнения первое и получаем
19х=57
х=19 далее находим у.