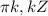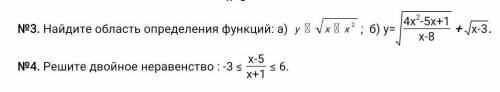
![3a)\ \ y=\sqrt{x-x^2}\ \ ,\ \ x-x^2\geq 0\ \ ,\ \ x(1-x)\geq 0\ \ ,\ \ \ x(x-1)\leq 0\ ,\\\\znaki:\ \ \ +++[\, 0\, ]---[\ 1\ ]+++\\\\x\in [\ 0\, ;\, 1\ ]](/tpl/images/1612/0613/22d0b.png)
![3b)\ \ y=\sqrt{\dfrac{4x^2-5x+1}{x-8}}+\sqrt{x-3}\ \ \ \Rightarrow \left\{\begin{array}{l}\dfrac{4x^2-5x+1}{x-8}\geq 0\\\\x-3\geq 0\end{array}\right\\\\\\\left\{\begin{array}{l}\dfrac{4(x-1)(x-\frac{1}{4})}{x-8}\geq 0\\\\x\geq 3\end{array}\right\ \ \left\{\begin{array}{l}x\in [\ \frac{1}{4}\ ;\ 1\ ]\cup (\, 8\, ;+\infty )\\x\geq 3\end{array}\righ\ \ \ \Rightarrow \ \ x\in (\ 8\ ;\, +\infty )](/tpl/images/1612/0613/eb5e0.png)
![4)\ \ -3\leq \dfrac{x-5}{x+1}\leq 6\ \ \ \Rightarrow \ \ \ \ \left\{\begin{array}{l}\dfrac{x-5}{x+1}\leq 6\\\dfrac{x-5}{x+1}\geq -3\end{array}\right\ \ \left\{\begin{array}{l}\dfrac{x-5}{x+1}-6\leq 0\\\dfrac{x-5}{x+1}+3\geq 0\end{array}\right\\\\\\\left\{\begin{array}{l}\dfrac{-5x-11}{x+1}\leq 0\\\dfrac{4x-2}{x+1}\geq 0 \end{array}\right\ \ \left\{\begin{array}{l}x\in (-\infty ;\ -2,2\ ]\cup (-1\, ;+\infty )\\x\in (-\infty \, ;\, -1\, )\cup [\ \dfrac{1}{2}\, ;+\infty )\end{array}\right\ \ \Rightarrow](/tpl/images/1612/0613/2c9d3.png)
![x\in (-\infty \, ;-2,2\ ]\cup [\ \dfrac{1}{2}\, ;+\infty )](/tpl/images/1612/0613/ef788.png)
1) Знак неравенства меняется если основное число меньше 1;
2) Если знак неравенства, то точка будет неполная;
3) Если знак неравенства больше равно, меньше равно, то точка будет полная.
4) Полная точка ( зарисованная внутри );
5) Неполная точка ( не зарисованная внутри );
6) Если знак неравенства, то скобка "(" ;
7) Если знак неравенства больше равно, меньше равно, то скобка
"[" ;
8) В какую сторону показывает носик неравенства, в ту сторону рисуем допустимые значения;
9) Не забываем что числа можно подавать как меньшее число в степени;
Теперь когда всё вспомнили можно решать:
1) 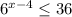
Подаём число 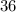 как
как 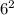
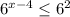
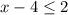
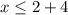
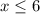
Не забываем что можно сократить основы если они одинаковые.
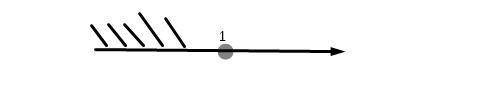
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Фото прямых прикрепил.
Точка полная так как имеем 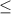 .
.
Допустимые значения направленные в левую сторону так как "носик" знака неравенства направлен именно туда.
x ∈ ( -∞, 6 ]
2) 
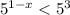
Подаём число 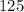 как
как 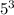
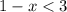
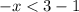
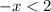
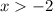
Сменили знак неравенства, так как перенесли - в другую часть неравенства.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем > .
x ∈ ( -2, +∞ )
3) 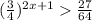
Подаём 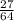 как
как 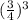 .
.
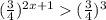
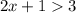
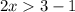
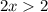
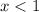
Сменили знак неравенства, так как 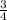 меньше 1.
меньше 1.
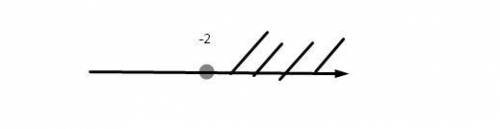
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем  .
.
x ∈ ( -∞, 1 )

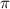 k, k ЄZ
k, k ЄZ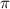 k, k ЄZ
k, k ЄZ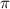 k, kЄZ
k, kЄZ 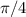 +
+ 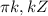
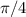 +
+