это я не знаю
Объяснение:
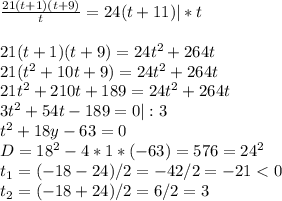
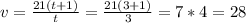 (км/ч)
(км/ч)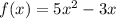 - квадратичная функция, графиком является парабола.
- квадратичная функция, графиком является парабола.
a = 5, a > 0, ветви параболы направлены вверх.
1) Для начала найдём область определения функции. Никаких дополнительных ограничений на аргумент не накладывается, поэтому: 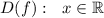 .
.
2) Найдём координаты вершины параболы. Её абсцисса: 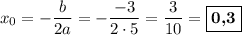 . Её ордината:
. Её ордината: 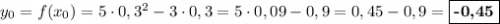 .
.
Таким образом, координаты вершины параболы: 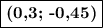 .
.
3) Найдём множество значений данной функции. Её график ограничен снизу, поэтому максимальное значение функции не определено, а минимальное соответствует ординате вершины параболы, значит:
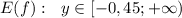 .
.
4) Осью симметрии параболы является прямая, проходящая через вершину параболы и параллельная оси ординат. Таким образом, осью симметрии графика данной функции является прямая 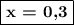 .
.
5) Нулями функции называются те значения аргумента, при которых функция обращается в ноль. Получаем:
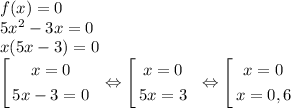
Таким образом, функция имеет два нуля:  и
и 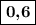 .
.
6) Промежутки знакопостоянства данной параболы напрямую зависят от нулей функции: на интервале от одного нуля до второго функция будет отрицательна, на всех остальных - положительна.
Функция положительна при 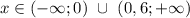 .
.
Функция отрицательна при 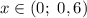 .
.
7) Промежутки монотонности - это промежутки возрастания и убывания. Для параболы они сменяют друг друга в вершине.
Функция убывает при ![x \in (-\infty;\ 0,3]](/tpl/images/1561/2119/ce593.png) .
.
Функция возрастает при 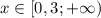 .
.
8) График пересекает ось Oy в тех точках, где 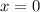 . Абсцисса известна, осталось найти ординату: просто подставляем значение в функцию.
. Абсцисса известна, осталось найти ординату: просто подставляем значение в функцию.
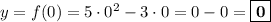 .
.
Таким образом, график данной функции пересекает ось Oy в точке с координатами 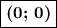 .
.
Объяснение:
Вот ответ на вопрос ен кушти ответ зашаш