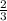(a-3b)/3=(3b- a)/4
4а-12в=9b-3a
7a=21b
a=3b
(a^2-b^2)/ab=((3b)^2-b^2)/3bb=b^2(3^2-1)/3b^2=(9-1)/3=8/3=2(2/3)
1) (sin(2t))/(1+cos(2t)) *((сost)/(1+cos(t)) =
(((2sint)*(cost))/(2cos²t))*(cost/(2cos²(t/2)))=(tgt)*cost/(2cos²(t/2))=
(sint)/(2cos²(t/2))=(2sin(t/2))*cos(t/2)/(2cos²(t/2))=tg(t/2)
Bоспользовался дважды формулой (1+cosα)=2cos²α ; формулой синуса двойного аргумента sin2α=2(sinα)*(cosα) и tgα=sinα/cosα.
2) Докажем второе тождество, используя те же формулы.
((sin(2t))/(1+cos(2t)))*(cost/(1+cost))*(cos(t/2))/(1+cos(t/2))=tg(t/4)
1) упростим ((sin(2t))/(1+cos(2t)))=(2sint)(сost)/(2cos²t)=sint/(cost)=tgt
2) умножим (tgt)*(cost/(1+cost))=(sint)/(2cos²(t/2))=
(2sin(t/2))*(cos(t/2))/(2cos²(t/2))=tg(t/2)
3) умножим (tg(t/2))*((cos(t/2))/(1+cos(t/2))=sin(t/2)/(2cos²(t/4)=
(2sin(t/4)*(cos(t/4))/(2cos²(t/4))=tg(t/4)
Требуемое доказано.
Запишем пропорцию
(а - 3в): 3 = (3в - а): 4
4(а - 3в) = 3(3в - а)
4а - 12в = 9в - 3а
7а = 21в
а = 3в
Подставим в выражение
(a² - в²)/aв = (9в² - в²):3в² = 8в²:3в² = 8:3 = 2