Решим пропорцией
1) 30 уч. - 100%
х уч. - 60%
30*60/100=18
18 девочек в классе
2) 18 уч.-60%
х уч. - 100%
18*100/60=30
30 учеников в классе
3)30 уч.-100%
18уч. - х%
18*100/30=60
60% девочек в классе
2у=6-3х
Какое уравнение не задает ту же прямую?
Объяснение:
Дано уравнение прямой:
3х-2у=6
1.
С тождественных преобразо
ваний получим:
3х-2у=6 | ×2
6х-4у=12
Полученное уравнение задает ту же
прямую, так как уравнения равносиль
ны:
3х-2у=6 <==> 6х-4=12
2.
3х-2у=6 <==>
-2у=6-3х | ×(-1) <==>
2у=-6+3х
Полученное уравнение не равносильно
заданному.
Ввод:
Это уравнение задает ДРУГУЮ прямую.
Уравнение 2у=6-3х задает другую прямую.
3.
3х-2у=6 | :3 <==>
3х/3-2у/3=6/3 <==>
х-2/3у=2
Последнее уравнение получено из задан
ного тождественным преобразованием,
поэтому уравнения равносильны. Это
уравнение задает ту же прямую.
4.
3х-2у=6 | :2 <==>
1,5х-у=3
Полученное уравнение равносильно исходному, поэтому это уравнение зада
ет ту же прямую.
О т в е т :
2у=6-3х
.
Объяснение:
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O1 и O2, а середины отрезков BD, DC, MN, DO2 и O1O2 — через A1, A2, K, E и O соответственно (см. рис.). Пусть ∠ BAD = ∠ CAD = α . Тогда ∠ A1O1D = ∠ A2O2D = α (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O1MNO2, следовательно, OK ⊥ l, и (фото сверху). Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.
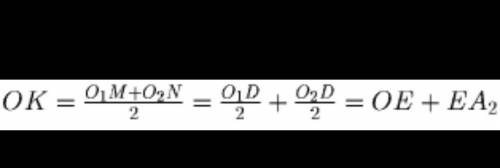
60%=0,6
1) 30*0,6=18 - девочек в классе
2) 18:0,6=30 - учеников в классе,
3) 18:30=0,6=60% - девочек в классе