Question

Математики очень надо сейчас сдать

Answer 1

а)

$\cos{6x} \geq -\dfrac{1}{2}\\\\\\-\dfrac{2\pi}{3} + 2\pi k \leq 6x \leq \dfrac{2\pi}{3} + 2\pi k\ \ \ \ \ \ \Big| : 6\\\\\\-\dfrac{\pi}{9} + \dfrac{\pi k}{3}\leq x \leq \dfrac{\pi}{9} + \dfrac{\pi k}{3}$

ответ:  $x\in\left[-\dfrac{\pi}{9} + \dfrac{\pi k}{3};\ \dfrac{\pi}{9} + \dfrac{\pi k}{3}\right]\ ,\ k\in\mathbb{Z}$ .

б)

$\left(\dfrac{1}{4}\right) ^{x^2 - 4}\leq 2^{x^2+1}\\\\\\\left(2^{-2}\right)^{x^2-4}\leq 2^{x^2+1}\\\\\\2^{-2(x^2-4)}\leq 2^{x^2+1}\\\\-2(x^2-4)\leq x^2 + 1\\\\-2x^2 + 8 \leq x^2 + 1\\\\-2x^2 - x^2 \leq 1 - 8\\\\-3x^2\leq -7\ \ \ \ \ \Big| :(-3)\\\\x^2 \geq \dfrac{7}{3}\\\\\\x^2 - \dfrac{7}{3} \geq 0\\\\\\\left(x - \sqrt{\dfrac{7}{3}}\right)\left(x+\sqrt{\dfrac{7}{3}}\right) \geq 0$

Преобразуем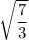 $\sqrt{\dfrac{7}{3}}$ :

$\sqrt{\dfrac{7}{3}} = \dfrac{\sqrt{7}}{\sqrt{3}} = \dfrac{\sqrt{7}\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}} = \dfrac{\sqrt{7\cdot 3}}{3} = \dfrac{\sqrt{21}}{3}$

Вернёмся к неравенству:

$\left(x - \dfrac{\sqrt{21}}{3}\right)\left(x+\dfrac{\sqrt{21}}{3}\right) \geq 0$

Решим неравенство методом интервалов:

           +                            -                              +

-----------------------$\bullet$-------------------------$\bullet$--------------------------> x

                     $-\dfrac{\sqrt{21}}{3}$                       $\dfrac{\sqrt{21}}{3}$

Так как неравенство имеет знак "больше или равно", то нам нужны те промежутки, где выражение имеет знак "плюс".

ответ:  $x\in\left(-\infty; -\dfrac{\sqrt{21}}{3}\right]\cup \left[\dfrac{\sqrt{21}}{3};+\infty\right)$