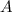можно выбрать 
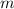и если после каждого такого выбора объект 
можно выбрать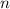 
то выбор пары 
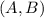в указанном порядке можно осуществить 
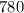
№1.
Отметим данные точки и проведём через них прямую.
Прямая пересекает ось Oy в точке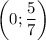 
; ось Ox в точке (1,25;0). Подробнее смотри в приложении.
№2.
Точка M(x;y):
расположена в 1 четверти, если x>0 и y>0;
расположена во 2 четверти, если x<0 и y>0;
расположена в 3 четверти, если x<0 и y<0;
расположена в 4 четверти, если x>0 и y<0.
Точка A(-87;89) расположена во 2 четверти т.к. -87<0 и 89>0.
Точка B(3,5;2) расположена в 1 четверти т.к. 3,5>0 и 2>0.
Точка C(0,1;-0,001) расположена в 4 четверти т.к. 0,1>0 и -0,001<0.
Точка D(-1,25;-3,48) расположена в 3 четверти т.к. -1,25<0 и -3,48<0.
In(x)/x²→∞, в то время x→0 слева, а
In(x)/x²→-∞, в то время как x→0 справа, следовательно, x=0- вертикальная асимптота.
x=0
Не принимая во внимание логарифм, рассмотрим рациональную функцию
R(x) = axⁿ/bx^m, где n- степень числителя, а m степень знаменателя.
1. если n<m, то ось x, y=0, является горизонтальной асимптотой.
2. если n=m, то горизонтальной асимптотой является прямая y= a/b
Если n>m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем m и n
n=0
m=2
Поскольку n<m, ось X, y=0
, является горизонтальной асимптотой.
y=0
Для логарифмических и тригонометрических функций не существует наклонных асимптот.
Нет наклонных асимптот
Это множество всех асимптот.
Вертикальные асимптоты: x=0
Горизонтальные асимптоты: y=0