Различные числа a и b делятся на c. Укажите термин false: a - b + 1 A) число делится на c; atb 2a - b B) сокращенная дробь; a + b C) число ab делится на c; D) Число Za + 2b делится на число c; E) ab - 2c делится на c.

Различные числа a и b делятся на c. Укажите термин false: a - b + 1 A) число делится на c; atb 2a -

👇

Увидеть ответ

Ответ:

zelenukanna2002

18.08.2020

а) ақиқат

в) жалған

с) ақиқат

д) жалған

е) ақиқат

4,5(37 оценок)

Открыть все ответы

Ответ:

Лиза200111111

18.08.2020

y = -6·x

Объяснение:

Пусть линейные функции, то есть прямые заданы уравнениями y₁=k₁·x+b₁ и y₂=k₂·x+b₂. Прямые параллельны тогда и только тогда, когда k₁=k₂ и b₁≠b₂. Если k₁=k₂ и b₁=b₂, то прямые совпадают.

В силу этого, уравнение прямой, параллельной графику функции y=-6·x+10 имеет вид: y=-6·x+b. Так как прямая проходит через начало координат О(0; 0), то подставляя эти значения определяем b:

0=-6·0+b или b=0.

Тогда уравнение прямой, параллельной графику функции y=-6x+10 и проходящей через начало координат имеет вид: y=-6·x.

4,6(21 оценок)

Ответ:

kapitoshka202

18.08.2020

$p(x)=a_{1}x^4+a_{2}x^3+a_{3}x^2+a_{4}x+a_{5}\\
 x=\sqrt{x_{1}}\\
 x=\sqrt{x_{1}}+b\\
 x=\sqrt{x_{1}}+2b\\
 x=\sqrt{x_{1}}+3b\\\\
 p(x)+a=a_{1}x^4+a_{2}x^3+a_{3}x^2 + a_{4}x+a_{5}+a\\
y=\sqrt{y_{1}}\\
y=\sqrt{y_{2}}\\
y=\sqrt{y_{3}}\\
y=\sqrt{y_{4}}\\\\ 


$

По теореме Виета для уравнение четвертой степени получаем соотношение
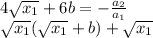
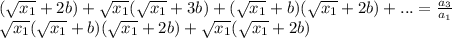
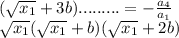
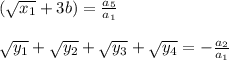
$4\sqrt{x_{1}}+6b = -\frac{a_{2}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)+\sqrt{x_{1}}$ $(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+3b)+(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+...=\frac{a_{3}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b).........=-\frac{a_{4}}{a_{1}} \\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b)=\frac{a_{5}}{a_{1}}\\\\ \sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}=-\frac{a_{2}}{a_{1}}\\$
\sqrt{y_{1}y_{2}}+\sqrt{y_{1}y_{3}}+\sqrt{y_{1}y_{4}}+\sqrt{y_{2}y_{3}}...+ = \frac{a_{3}}{a_{1}} \\ \sqrt{y_{1}y_{2}y_{3}}+\sqrt{y_{1}y_{2}y_{4}} [/tex]

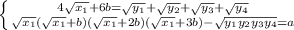
$\left \{ {{4\sqrt{x_{1}}+6b=\sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}
 } \atop {\sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)(\sqrt{x_{1}}+3b)-\sqrt{y_{1}y_{2}y_{3}y_{4}}=a} \right. \\
$
Учитывая условия что коэффициенты все выражаются в радикалах , то сумма всех корней выраженные в радикалах есть число радикальное .
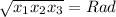По третьем равенству первой системы $\sqrt{x_{1}x_{2}x_{3}}=Rad$ , то произведение корней так же число радикальное , откуда с последних двух идет верное равенство