7) В уравнении |x - 1|=k, вместо k напишите такое число, чтобы уравнение: а) не имело решений; b) имело два действительных корня, с) имело три действительных корня, d) имело четыре действительных корня.
1) 10a + b = a + b^2 10a - a = b^2 - b 9a = b*(b - 1) Есть варианты: а) b = 9; a = b - 1 = 8; a + b = 8 + 9 = 17 б) b - 1 = 9; a = b = 9 + 1 = 10 - не может быть. в) b = 3; b - 1 = 2 = 3a - не может быть. г) b - 1 = 3; b = 4 = 3a - не может быть. Других вариантов быть не может. ответ: 17
2) 44^5 * 55^12 = 4^5*11^5 * 5^12*11^12 = 4^5*5^10*5^2*11^17 = = (4*25)^5*25*11^17 = A 11^17 ~ 5*10^18 A = 100^5*25*5*10^18 = 125*10^28 Это число имеет 30 знаков.
3) Не понятно, что такое k2x. Может, это k в квадрате, умноженное на x? Или что-то другое?
4) |3 - x| + |2x + 4| - |x + 1| = 2x + 4 Это уравнение можно свести к |3 - x| = x + 1 У него только один корень: x = 1 ответ: 1 корень
Ищем общее решение однородного уравнения y'' - 3y' = 0 в виде y = exp(λx). Подставляя, получаем характеристическое уравнение λ^2 - 3λ = 0, откуда λ = 0 или λ = 3. Общее решение однородного уравнения yo = A + Bexp(3x).
Решение неоднородного уравнения ищем в виде y1 = ax^3 + bx^2 + cx + d. Подставляем: 6ax + 2b - 9ax^2 - 6bx - 3c = 9x^2 + 1 Приравнивая коэффициенты при равных степенях, получаем -9a = 9 6a - 6b = 0 2b - 3c = 1
a = -1 b = -1 c = -1
В качестве частного решения можно взять y1 = -x^3 - x^2 - x.
Общее решение неоднородного уравнения - сумма частного решения неоднородного уравнения и общего решения однородного.
c) , d) уравнение не может иметь ни 3, ни 4 действительных корня
Можно записать k=0, и тогда уравнение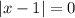 будет иметь 1 действительный корень .
будет иметь 1 действительный корень .
Cмотри рисунок .