Дана функция 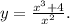
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
Дана функция 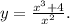
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
Объяснение:
S = ab -площадь
a - длина b - ширина
а = b +6
P = 2 (a+b) - периметр
условие 2 (a+b)> 24
ab < 72
Если а = b +6
тогда S = ( b+6) b < 72
b^2 +6 b < 72
b^2 +6 b -72 < 0
Д = 36 - 4*-72 = 36+288 = 324
√Д = √324 = 18
b 1 = (-6 +18)/2 = 6 см
b 2 = (-6-18)/2 = -12 - не подходит b <0
a = 6+6 = 12 см.
а < 12, b <6
0 < a < 12
0 < b < 6
Если а = b +6
тогда P = 2(b+6+b) > 24
P = 4 b +12 >24
4 b > 12
b >3
тогда a > 3+3 = 6
a > 6
Итого: 6 < a < 12
3 < b < 6