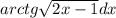
![\int arctg\sqrt{2x-1}\, dx=\Big[\ t^2=2x-1\ ,\ t=\sqrt{2x-1}\ ,\ x=\dfrac{t^2+1}{2}\ ,\ dx=t\, dt\Big]=\\\\\\=\int arctgt\cdot t\, dt=\Big[\ u=arctgt\ ,\ du=\dfrac{dt}{1+t^2}\ ,\ dv=t\, dt\ ,v=\dfrac{t^2}{2}\ ,\\\\\\\int u\, dv=uv-\int v\, du\ \Big]=\dfrac{t^2}{2}\cdot arctgt-\dfrac{1}{2}\int\dfrac{t^2\, dt}{1+t^2}=\\\\\\=\dfrac{t^2}{2}\cdot arctgt-\dfrac{1}{2}\int\Big(1-\dfrac{1}{1+t^2}\Big)\, dt=\dfrac{t^2}{2}\cdot arctgt-\dfrac{1}{2}\cdot \Big(t-arctgt\Big)+C=](/tpl/images/1615/5538/1ad2b.png)
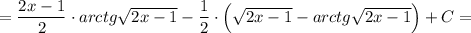
ответ:
объяснение:
здесь область допустимых значений состоит только из двух
под первым корнем квадратный трехчлен --парабола, ветви вверх:
2x²-8x+6 ≥ 0
x²-4x+3 ≥ 0 корни: 1 и 3 (по теореме виета)
решение: х ∈ (-∞; 1] u [3; +∞)
под вторым корнем квадратный трехчлен --парабола, ветви вниз:
-x²+4x-3 ≥ 0
x²-4x+3 ≤ 0 корни те же))
решение: х ∈ [1; 3]
пересечением этих двух промежутков (условия должны выполняться одновременно) будет множество из двух точек: х ∈ {1; 3}
легко проверить, что х=1 решением не является, т.к. сумма двух неотрицательных чисел (это квадратные корни) не может быть < 1-1 (меньше нуля)
остается х = 3: √0 + √0 < 3-1 это верно))
ответ: х=3
ответ: ('-')
_стройте быстрее ! |__/
('_') / | |
_|_ | y = v / \
| |
/ \ || x+2
/ { -1; 7 }
('_')_/ /
|__/
|
/ \