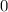 до
до 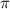 (верхняя полуплоскость числовой окружности) косинус убывает от
(верхняя полуплоскость числовой окружности) косинус убывает от  до
до  .
.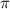 до
до 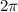 (нижняя полуплоскость числовой окружности) косинус возрастает от
(нижняя полуплоскость числовой окружности) косинус возрастает от  до
до 
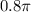 и
и 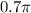 на числовой окружности лежит в верхней полуплоскости. Так как
на числовой окружности лежит в верхней полуплоскости. Так как 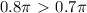 , то
, то 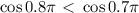
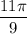 и
и 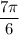 на числовой окружности лежит в нижней полуплоскости. Сравним:
на числовой окружности лежит в нижней полуплоскости. Сравним: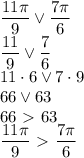
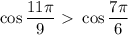
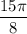 и
и 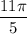 расположены в 4 и 1 четвертях соответственно. Преобразуем выражения так, чтобы углы располагались в одной полуплоскости:
расположены в 4 и 1 четвертях соответственно. Преобразуем выражения так, чтобы углы располагались в одной полуплоскости:
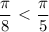 . Значит,
. Значит, 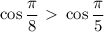 , следовательно
, следовательно 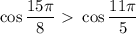

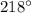 и
и 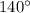 расположены в 3 и 2 четвертях, поэтому преобразуем первое выражение:
расположены в 3 и 2 четвертях, поэтому преобразуем первое выражение: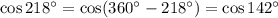
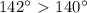 . Тогда,
. Тогда, 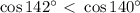 или
или 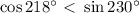
если cos x=-1, то sin^2 x = 1-cos^2 x = 1-1 = 0, т.е. sin x=0.
Решений нет.