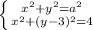
Найдите наименьшее значение параметра а, при котором представленная система имеет одно решение? $\left \{ {{x^{2} + y^{2} = a^{2} } \atop {x^{2} + (y-3)^{2} = 4}} \right.$

👇

Открыть все ответы

Ответ:

golubfrog

17.04.2023

Интересная задачка.

Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов:
Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.

4,7(88 оценок)

Ответ:

mario160

17.04.2023

{x=6

y=2

z=5

Объяснение:

Метод Крамера:

Δ= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$ =2*(-3)*(-1)+1*2*3+(-3)*1*(-4)-(-3)*(-3)*3-1*1*(-1)-2*2*(-4)=14

Δx= $\left[\begin{array}{ccc}-1&1&-3\\10&-3&2\\5&-4&-1\end{array}\right]$ =(-1)*(-3)*(-1)+1*2*5-3*10*(-4)-(-3)*(-3)*5-1*10*(-1)+1*2*(-4)=84

Δy= $\left[\begin{array}{ccc}2&-1&-3\\1&10&2\\3&5&-1\end{array}\right]$ =2*10*(-1)+(-1)*2*3+(-3)*1*5-(-3)*10*3-(-1)*1*(-1)-2*2*5=28

Δz= $\left[\begin{array}{ccc}2&1&-1\\1&-3&10\\3&-4&5\end{array}\right]$ =2*(-3)*5+1*10*3+(-1)*(-4)*1-(-1)*(-3)*3-1*1*5-2*10*(-4)=70

x=Δx/Δ=84/14=6

y=Δy/Δ=28/14=2

z=Δz/Δ=70/14=5

Метод Гаусса

$\left[\begin{array}{cccc}2&1&-3&-1\\1&-3&2&10\\3&-4&1&5\end{array}\right]$

Делим первую строку на 0,5(r1/0.5)

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\1&-3&2&10\\3&-4&1&5\end{array}\right]$

Далее r3-3r1 и r2-r1

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\0&-3,5&3,5&10,5\\0&-5,5&3,5&6,5\end{array}\right]$

Следующая итерация r2/(-3.5)

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\0&1&-1&-3\\0&-5,5&3,5&6,5\end{array}\right]$

cледующий шаг r1-0.5r2 И r3+5.5r2

$\left[\begin{array}{cccc}1&0&-1&1\\0&1&-1&-3\\0&0&1&5\end{array}\right]$

Последний шаг r1+r3 r2+r3

$\left[\begin{array}{cccc}1&0&0&6\\0&1&0&2\\0&0&1&5\end{array}\right]$

{x=6 y=2 z=5

Матричный метод

A= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$

Δ= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$ =2*(-3)*(-1)+1*2*3+(-3)*1*(-4)-(-3)*(-3)*3-1*1*(-1)-2*2*(-4)=14

Находим миноры:

M11= $\left[\begin{array}{cc}-3&2\\-4&-1\end{array}\right]$ =11

M12= $\left[\begin{array}{cc}1&2\\3&-1\end{array}\right]$ =-7

М13= $\left[\begin{array}{cc}1&-3\\3&-4\end{array}\right]$ =5

M21= $\left[\begin{array}{cc}1&-3\\-4&-1\end{array}\right]$ =-13

M22= $\left[\begin{array}{cc}2&-3\\3&-1\end{array}\right]$ =7

M23= $\left[\begin{array}{cc}2&1\\3&-4\end{array}\right]$ =-11

M31= $\left[\begin{array}{cc}1&-3\\-3&2\end{array}\right]$ =-7

M32= $\left[\begin{array}{cc}2&-3\\1&2\end{array}\right]$ =7

M33= $\left[\begin{array}{cc}2&1\\1&-3\\\end{array}\right]$ =-7

A11=11 A12=7 A13=5

A21=12 A22=7 A23=11

A31=-7 A32=-7 A33=-7

A*= $\left[\begin{array}{ccc}11&7&8\\13&7&11\\-7&-7&-7\end{array}\right]$

A*т= $\left[\begin{array}{ccc}11&13&-7\\7&7&-7\\5&11&-7\end{array}\right]$

A-1= A*т/Δ= $\left[\begin{array}{ccc}11/14&13/14&-1/2\\1/2&1/2&-1/2\\5/14&11/14&-1/2\end{array}\right]$

X=A-1*B

B= $\left[\begin{array}{c}-1\\10\\5\end{array}\right]$

X= $\left[\begin{array}{ccc}11/14&13/14&-1/2\\1/2&1/2&-1/2\\5/14&11/14&-1/2\end{array}\right]$ * $\left[\begin{array}{c}-1\\10\\5\end{array}\right]$ = $\left[\begin{array}{c}11/14*(-1)+13/14*10-1/2*5\\1/2*(-1)-1/2*10-1/2*5\\5/14*(-1)+11/14*10-1/2*5\end{array}\right]$ = $\left[\begin{array}{c}-11/14+65/7-5/2\\-1/2+5-5/2\\-5/14+55/7-5/2\end{array}\right]$ = $\left[\begin{array}{c}6\\2\\5\end{array}\right]$