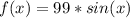 это растянутый вдоль оси OY в 99 раз график функции
это растянутый вдоль оси OY в 99 раз график функции 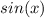 , нужно отметить, что функциия
, нужно отметить, что функциия 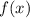 - нечётная функция и проходит через точку
- нечётная функция и проходит через точку 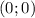
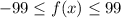
 - обычная себе прямая линия, с наклоном
- обычная себе прямая линия, с наклоном 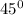 к оси ОХ, также проходящая через точку
к оси ОХ, также проходящая через точку 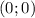
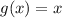 будет пересекать "гребни" функции
будет пересекать "гребни" функции 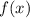 , начиная с значения -99 и пока её значение не привысит 99, а это случиться, на промежутке
, начиная с значения -99 и пока её значение не привысит 99, а это случиться, на промежутке ![x\in[-99;99]](/tpl/images/0891/3109/35ccc.png)
![x\in[0;99]](/tpl/images/0891/3109/c8611.png) прямая линия пересекает только "положительные гребни" синусоиды при чем на один период есть только один положительный гребень, и каждый гребень эта прямая линия будет пересикать в двух точках. Сколькои таких гребней, столько и периодов на промежутке
прямая линия пересекает только "положительные гребни" синусоиды при чем на один период есть только один положительный гребень, и каждый гребень эта прямая линия будет пересикать в двух точках. Сколькои таких гребней, столько и периодов на промежутке ![x\in[0;99]](/tpl/images/0891/3109/c8611.png) :
: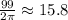
![x\in[-99;0]](/tpl/images/0891/3109/59366.png) (точки пересечения будут уже с "отрицательными гребнями" синусоиды) - 32 точки пересечения
(точки пересечения будут уже с "отрицательными гребнями" синусоиды) - 32 точки пересечения![x\in[-99;99]](/tpl/images/0891/3109/35ccc.png) будет на одну точку пересечения меньше, потому как точка пересечения
будет на одну точку пересечения меньше, потому как точка пересечения 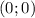 учитывалась в обоих промежутках
учитывалась в обоих промежутках
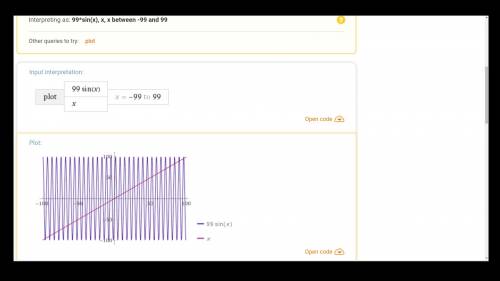
В решении.
Объяснение:
Объяснение:
Найдите сумму и разность многочленов А и В. Запишите результат как многочлен стандартного вида.
1) Записать в одну строку, второй многочлен в скобках, между ними знак + или -.
2)Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3)Привести подобные члены.
4)Записать результат в стандартном виде, т.е., в порядке убывания степеней.
а) 5х² - 0,18у³ + (6,2х² + 7у³)=
=5х² - 0,18у³ + 6,2х² + 7у³=
=6,82у³ + 11,х²;
б) 5х² - 0,18у³ - (6,2х² + 7у³)=
=5х² - 0,18у³ - 6,2х² - 7у³=
= -7,18у³ - 1,2х².