
Задание №1.
1. На березе растут яблоки - Невозможное.
2. При бросании игральной кости выпала цифра 6 - Равновозможное.
3. За летом наступает осень - Достоверное.
Задание №2.
Всего двухзначных чисел у нас - 90 (от 10 до 99). Проще всего рещать в лоб, выбирая подходящие числа:
1) Нулём оканчивается каждое десятое из них, т.е. всего таких чисел 9. P = 9/90=0,1
2) Из одинаковых цифр состоит каждое одиннадцатое из них, начиная с 11, т.е. всего таких чисел 9. P = 9/90=0,1
3) Больше 27 и меньще 46 - всего 18 чисел, т.е. P =18/90=0,2
4) Квадратами целого числа являются 16, 25, 36, 49, 64, 81 - итого 6. P = 6/90=1/15
Задание №3.
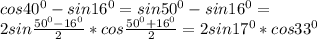
Объяснение:
(3*a+1)^2=9*a^2+6*a+1
>9*a^2+6*a-3=9(а-1/3)(a+1)
Квадратное уравнение, решаем относительно a:
Ищем дискриминант:D=6^2-4*9*(-3)=36-4*9*(-3)=36-36*(-3)=36-(-36*3)=36-(-108)=36+108=144;
Дискриминант больше 0, уравнение имеет 2 корня:a_1=(√144-6)/(2*9)=(12-6)/(2*9)=6/(2*9)=6/18=1/3;a_2=(-√144-6)/(2*9)=(-12-6)/(2*9)=-18/(2*9)=-18/18=-1.
Выражение: 9-(2-5*b)^2
(2-5*b)^2=4-20*b+25*b^2
>5+20*b-25*b^2=-25(a+1/5)(a-1)
Квадратное уравнение, решаем относительно b:
Ищем дискриминант:D=20^2-4*(-25)*5=400-4*(-25)*5=400-(-4*25)*5=400-(-100)*5=400-(-100*5)=400-(-500)=400+500=900;
Дискриминант больше 0, уравнение имеет 2 корня:b_1=(√900-20)/(2*(-25))=(30-20)/(2*(-25))=10/(2*(-25))=10/(-2*25)=10/(-50)=-10/50=-(1/5)~~-0.2;b_2=(-√900-20)/(2*(-25))=(-30-20)/(2*(-25))=-50/(2*(-25))=-50/(-2*25)=-50/(-50)=-(-50/50)=-(-1)=1.