Question

Найдите значения выражения cos2α - sin2α , если tgα=2.

Answer 1

Если я правильно понял задание, то даны косинус и синус двойного угла. Если да. То начнем по порядку:
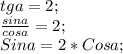
1- Нам дан тангенс - это отношение синуса к косинусу. Запишем:
$tga=2;\\ \frac{sina}{cosa}=2;\\ Sina=2*Cosa;\\$

Теперь распишем само выражение, применяя формулы синуса и косинуса двойного угла:
$Sin2a=2sina*cosa;\\ cos2a=cos^2(a)-sin^2(a);\\ Cos2a-sin2a=cos^2(a)-sin^2(a)-2sina*cosa;\\$

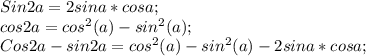
Воспользуемся нашим отношением (Sina=2cosa).

Подставим значение косинуса в наше выражение:
$Cos2a-sin2a=cos^2(a)-sin^2(a)-2sina*cosa=\\ Cos^2(a)-(2cosa)^2-2*2*cosa*cosa=cos^2(a)-4cos^2(a)-\\-4cos^2(a)=cos^2(a)-8cos^2(a)=-7cos^2(a);\\$

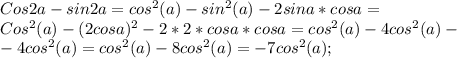
2-Также мы знаем формулу:

$1+tg^2(a)=\frac{1}{cos^2(a)};\\$

Откуда получим cos^2(a):

$1+4=\frac{1}{cos^2(a)};\\ 5*cos^2(a)=1;\\ cos^2(a)=\frac{1}{5};\\$

Подставим в наше выражение:

$-7cos^2(a)=-7*\frac{1}{5}=-\frac{7}{5};\\$

Вот и получили ответ.

Если же в дано идет Cos^2(a)-sin^2(a) - то получим:

$Cos^2(a)-sin^2(a)=cos^2(a)-(1-cos^2(a))=cos^2(a)-1+cos^2(a)\\=2cos^2(a)-1;$
Воспользуемся полученным ранее, что Cos^2(a)=1/5;

$cos^2(a)-1+cos^2(a)=2cos^2(a)-1=2*\frac{1}{5}-1=\frac{2}{5}-\frac{5}{5}=-\frac{3}{5};\\$

Так же получили ответ.