![16)\int\limits {x}^ {\frac{2}{3} } dx = \frac{ {x}^{ \frac{5}{3} } }{ \frac{5}{3} } + c = \\ = \frac{3}{5} x \sqrt[3]{ {x}^{2} } + c](/tpl/images/1620/3394/a3c7c.png)
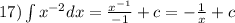
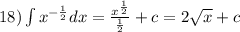
![19)\int\limits {x}^{ - \frac{2}{3} } dx = \frac{ {x}^{ \frac{1}{3} } }{ \frac{1}{3} } +c = 3 \sqrt[3]{x} + c \\](/tpl/images/1620/3394/411c8.png)
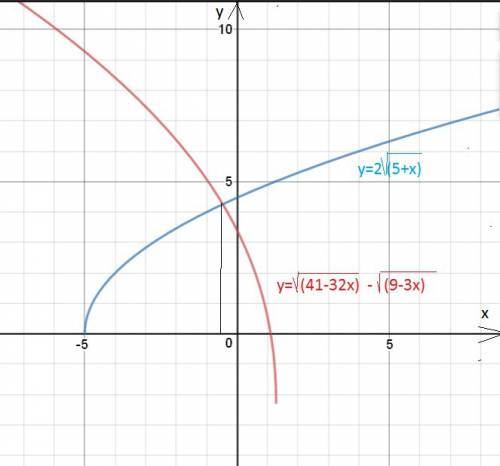
41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения