Объяснение:
а) х=2 это вертикальная асимптота. Это точка разрыва, т. е. это будет та точка, в которой знаменатель равен 0, т.к. на 0 делить нельзя. Следовательно
2·2+b=0; b=-4
y=3 - это горизонтальная асимптота. К этому значению стремится предел функции. Тогда
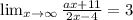
Применяя правило Лопиталя, будем иметь
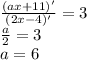
b)
i)
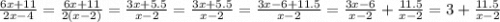
Как видим, к требуемому виду функция не приводится, т.к. 3≠-2
ii) В точках пересечения с осью у абцисса равна 0. Подставляем в уравнение, находим у:
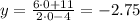
A(0;-2.75) - точка пересечения с осью у
В точках пересечения с осью х ордината равна 0. Решаем уравнение
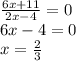
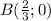 - точка пересечения с осью х.
- точка пересечения с осью х.
iii) Дополнительно исследуем функцию в точке разрыва
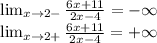
Схематически строим график

Отже ми маємо вираз х²+2х+2.
х²+2х+2= (х²+2х+1)+1= (х+1)²+1.
Вираз (х+1)² > 0 завжди, тому що в квадраті. 1>0 також, отже х²+2х+2>0 при х Є R. Довели.
Пам'ятаємо, що х²+2х+2= (х+1)²+1.
Найменшим значенням (х+1)² буде 0, коли х= -1. Тоді найменше значення всього виразу буде (-1+1)²+1= 0+1=1. (один при х= -1)