В решении.
Объяснение:
1)
а) х² + 3х⁴ = х²(1 + 3х²);
б) 3а² - 27 = 3(а² - 9) = 3(а - 3)(а + 3);
в) 2х + 4 + х² + 2х = х² + 4х + 4 = (х + 2)² = (х + 2)(х + 2).
2) х² - 3х = 0
х(х - 3) = 0
х₁ = 0;
х - 3 = 0
х₂ = 3.
3) 3abc⁸/a³bc² = 3c⁶/a².
4) 2ab - (a + b)² + 2a² =
= 2ab - (a² + 2ab + b²) + 2a² =
= 2ab - a² - 2ab - b² + 2a² =
= a² - b² =
= (a - b)(a + b);
(a - b)(a + b) = (a - b)(a + b), доказано.
5) х³ + 3х² - 9х - 27 = 0
(х³ + 3х²) - (9х + 27) =
= х²(х + 3) - 9(х + 3) =
= (х + 3)(х² - 9) =
= (х + 3)(х - 3)(х + 3) = 0
х + 3 = 0
х₁ = -3;
х - 3 = 0
х₂ = 3;
ответ:48
Объяснение: пусть d-это разность прогрессии и так же мы знаем такую формулу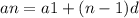
из нее выйдет что 1) 
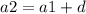= 12 и 2)
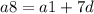= 16 вычтем из первого выражения второе тогда выйдет a1-a1+d-7d=-4 => 6d=4 тогда d=2/3 дальше что бы узнать какое число является членом прогрессии это не сложно мы знаем что n это всегда натуральное число так как номер члена прогрессии и он не может быть отрицательным выведем это в формуле 
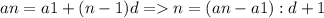всегда должно быть натуральным числом подставим в эту формулу первое число n=(48-12):2/3+1=25 это верно так как n натуральное число an=48 ; n=(208-12):2/3+1=395/3 не верно an≠208 ; n=(44-12):2/3+1=67/3 не верно ; n=(176-12):3/2+1=331/3 неверно тогда верный вариант ответа это 48