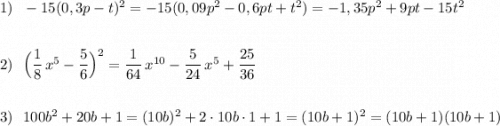
В решении.
Объяснение:
1.
-15(0,3p-t)^2 = -15(0,09p^2 - 0,6pt + t^2) = -1,35p^2 - 9pt + 15t^2.
2.
(1/8 x^5 - 5/6)^2 = 1/64 x^10 - 5/24 x^5 + 25/36.
3.
100b^2 + 20b + 1 = (10b + 1)^2 = (10b + 1)(10b + 1).
Объяснение:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним.
2. При делении степеней с одинаковыми основаниями основание остаётся прежним, а из показателя числителя вычитают показатель знаменателя.
3.При возведении степени в степень основание остаётся прежним а показатели перемножают.
4. При возведении в степень произведения, возводят в эту степень каждый множитель и результаты перемножают.
5. Степень числа а не равного нулю с нулевым показателем равна 1
Объяснение:
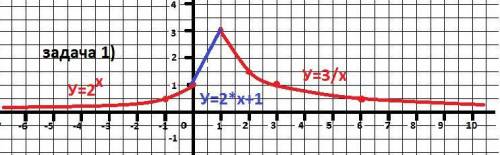
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
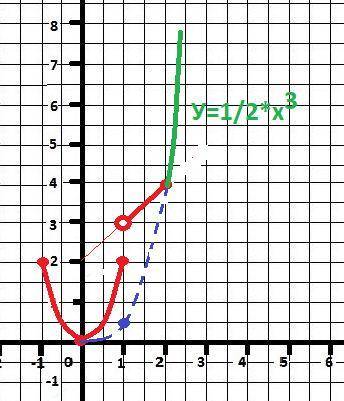
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.