1.
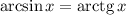
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
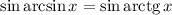
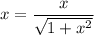
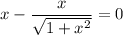
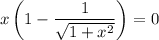
Уравнение распадается на два. Для первого уравнения получим:
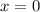
Решаем второе уравнение:
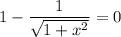
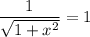
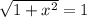
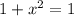
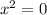
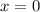
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
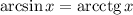
ОДЗ: арксинус определен при
Найдем синус левой и правой части:
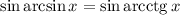
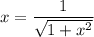
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть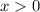 
.
Возведем в квадрат обе части:
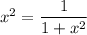
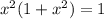
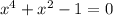
Решим биквадратное уравнение:
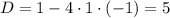
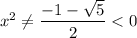
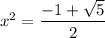
Находим х:
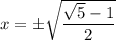
Однако, так как было выявлено ограничение 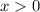, то отрицательный корень не попадает в ответ.
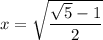
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:
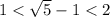
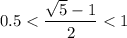
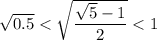
ответ: 
В решении.
Объяснение:
с -3 -2 -1
2с +3 2*(-3)+3= -3 2*(-2)+3= -1 2*(-1)+3 = 1
2(с+3) 2*(-3+3)=0 2*(-2+3)=2 2*(-1+3)=4
(2с)²-3 (2*-3)²-3=33 (2*-2)²-3=13 (2*-1)²-3=1
2(с²-3) 2*((-3)²-3)=12 2*((-2)²-3)=2 2*((-1)²-3)= -4
с 0 1 2 3
2с+3 0+3=3 2*1+3=5 2*2+3=7 2*3+3=9
2(с+3) 2*(0+3)=6 2*(1+3)=8 2*(2+3)=10 2*(3+3)=12
(2с)²-3 (2*0)²-3= -3 (2*1)²-3=1 (2*2)²-3=13 (2*3)²-3=33
2(с²-3) 2*(0²-3)= -6 2*(1²-3)= -4 2*(2²-3)=2 2*(3²-3)=12