1) по теореме косинусов имеем: a² = b² + c² - 2bc cos a = 25 - 24 cos 135° = 25 + 12√2 a = √(25 + 12√2) по теореме синусов, a / sin a = b / sin b sin b = sin a · b / a = √2 / 2 · 3 / √(25 + 12√2) = 3 / √(50 + 24√2) ∠b = arcsin(3 / √(50 + 24√2)) ∠c = 180° - 135° - ∠b = 45° - arcsin(3 / √(50 + 24√2)) 2) ∠a = 180° - ∠b - ∠c = 65° по теореме синусов b / sin b = a / sin a b = a sin b / sin a = 24.6 · √2 / 2 / (sin 65°) = 123√2 / (10 sin 65°) по теореме синусов c / sin c = a / sin a c = a sin c / sin a = 24.6 ·sin 70° / sin 65°
1) Произведение равно нулю, когда хотя бы один из множителей равен нулю, а другой при этом существует (x - 1)^2*(x + 2) = 0 (x - 1)^2 = 0 x - 1 = 0 x = 1
x + 2 = 0 x = - 2
2) Произведение равно нулю, когда хотя бы один из множителей равен нулю, а другой при этом существует (x^2 - 1)(x - 3) = 0 x^2 = 1 x₁ = 1 x₂= - 1;
x - 3 = 0 x₃ = 3
3) Произведение равно нулю, когда хотя бы один из множителей равен нулю, а другой при этом существует (x - 4)^2*(x - 3) = 0 x - 4 = 0 x = 4
x - 3 = 0 x = 3
4) Произведение равно нулю, когда хотя бы один из множителей равен нулю, а другой при этом существует (x^2 - 4)(x + 1) = 0
1)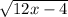
ответ: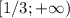
2)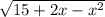
-x^2+2x+15=0
-1+-√1+15
x=----------------
-1
-1+-4
x=------------
-1
x=5
x=-3
5 + 2x - x^2= - (x-5) (x+3)
x=5 x=-3
ответ:![(-\infty; 3] \cup [5,+\infty)](/tpl/images/0162/8307/e731a.png)
3)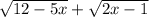
ответ:![[0,5; 2,4]](/tpl/images/0162/8307/e0288.png)