Оқулық Алгебра 8 сынып А.Е.Әбілқасымова, Т.П.Кучер, З.Ә.Жұмағұлова, В.Е.Корчевский. Мектеп - 2018 Өздігіңнен - id1630282020230506 от blazhenko66 06.05.2023 04:56

Question

Алгебра: Оқулық Алгебра 8 сынып А.Е.Әбілқасымова, Т.П.Кучер, З.Ә.Жұмағұлова, В.Е.Корчевский. Мектеп - 2018 Өздігіңнен орында: №12.7 және №12.8 Дескриптор: 1.Есеп шартын түсініп оқиды; 2.Ізделінді шаманы анықтап, қандай да бір айнымалымен белгілейді. 3.Есептің берілгендері мен ізделінді шамалар арасындағы тәуелділікті анықтап,  формула түрінде жазады. 4.Теңдеуді құрастырады, яғни бір шаманы өрнектейтін екі өрнекті теңестіреді. 5. Алынған теңдеудің түбірлерін табады. 6.Теңдеуден шыққан түбірлердің есептің

blazhenko66 · Accepted Answer

Если прямая перпендикулярно плоскости, то ее направляющий вектор является нормальным вектором плоскости.

1)Уравнение плоскости через нормальный вектор: Ax+By+Cz+D=0

, где A, B, C - координаты нормального вектора плоскости N(A,B,C).
Уравнение данной плоскости 2x-3y+4z-3=0

⇒ N(2,-3,4).

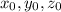2)Уравнение прямой через точку направляющий вектор: $\frac{x-x_{0}}{l}=\frac{y-y_{0}}{m}=\frac{z-z_{0}}{n}$ , где $x_{0},y_{0},z_0}$ - координаты точки M( 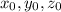$x_{0},y_{0},z_0}$ ), через которую проходит прямая, l,m,n

- координаты направляющего вектора S( l,m,n

).
По условию S( l,m,n

) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).

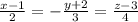
3)Готовое уравнение прямой: $\frac{x-1}{2}=-\frac{y+2}{3}=\frac{z-3}{4}$

MOGZ ответил