Допустимые значения переменной "х" - это те значения, которые брать можно. А что значит: можно? Когда говорят про допустимые значения переменной "х", то имеют в виду такие значения, при которых данный пример решается ( можно вычислить ответ. И мы должны помнить, что иногда действия выполнить нельзя (делить на 0 нельзя и т.д.)) а)(5у -8)/11 в этом выражение есть умножение, вычитание и деление на 11. Все эти действия выполняются при любом "у" ответ: у - любое б)25/(у - 9) В этом выражении есть вычитание и деление. вычитание можно выполнить при любом "у", а вот делить на 0 нельзя. ответ: у ≠ 9 в) (у² +1)/(у² -2у) И здесь есть деление. посмотрим когда знаменатель = 0 у² - 2у = 0 у(у -2) = 0 у = 0 или у - 2 = 0 у = 2 ответ: у ≠ 0 ; у ≠ 2
Биквадратное уравнение.
Решается заменой переменной:
Если D >0, т.е.
уравнение имеет корни:
Обратный переход:
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Аналогично
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Если , т.е
, т.е 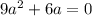
При
уравнение принимает вид:
уравнение не имеет корней
При
уравнение принимает вид:
Уравнение 4-ой степени, значит
О т в е т. При