Итак, нам нужно найти расстояние между пунктами А и В. Давайте его сразу и обозначим за 
(километров).
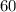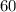км/ч. То есть, нам известно расстояние, которое проехал автомобиль (оно равно ) и его скорость ( км/ч). Вопрос: что мы можем найти? Конечно же, время. Оно равно пройденному расстоянию, деленному на скорость: 
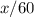(часов).А давайте теперь попробуем определить время, затраченное автобусом. Расстояние будет таким же - ровно километров, но двигаться наш транспорт будет помедленнее - со скоростью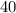 
км/ч. При этом находить время мы будем также: 
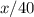(часов).Нам известно (ну или почти известно...) время, затраченное обоими видами транспорта на путь. Только что теперь с этим делать?
В условии сказано: "автомобиль приехал в пункт В на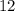 
минут раньше автобуса". Задумаемся: автомобиль ехал 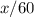часов, а автобус - 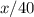часов. И, по условию, разность этих двух чисел равна 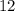минут. Это и есть ключевой момент задачи!
(!) Только не стоит торопиться! 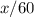и 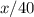мы измеряли в часах, и было бы странно в виде разности получить минуты. Так что не будем лишний раз испытывать умение решать уравнения и переведем 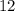минут в часы. Наверное, в часе 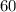минут (пусть это в задаче и не оговорено), поэтому 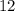минут - это 
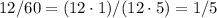часа.
Значит, имеем уравнение: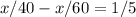 
(вычитаем именно из 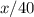, так как это - время автобуса, и, разумно предположить, что оно больше времени автомобиля).
Ничего иного не остается, кроме как решить полученное уравнение:
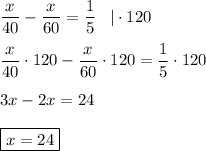
Это и есть ответ задачи!
Для уверенности можем сделать проверку:
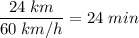(время автомобиля);
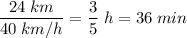(время автобуса);
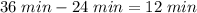(разность).Все сходится, задача решена!
Если останутся вопросы по такому виду задач, задавайте!
ответ:24 километра.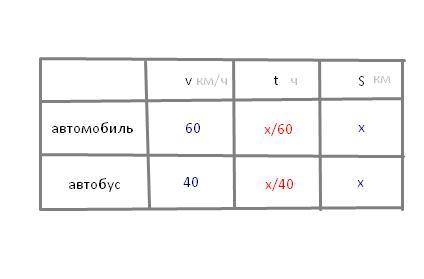
y(y+6)²-(y+1)(y-6)²=y(y²+12y+36)-(y+1)(y²+12y+36)=
=y³+12y²+36y-(y³+12y²+36y+y²+12y+36)=y³+12y²+36y-y³-12y²-36y-y²-12y-36=
=-y²-12y-36=-(y²+12y+36)=-(y+6)²
100-140a+49a²=(10-7a)²
x⁴+18x²y+81y²=(x²+9y)²
(x²-4x)²-16 =(x²-4x)²-4²=((x²-4x)+4)((x²-4x)-4)=(x²-4x+4)(x²-4x-4)
9b²-25c²-3b+5c=(9b²-25c²)+(-3b+5c)=(3b+5c)(3b-5c)-(3b-5c)=
=(3b-5c)(3b+5c-1)
(a-3b)²=a²-9b²
a²-3ab+9b²=a²-9b²
a²-6ab+9b²-a²+9b²=0
-6ab+18b²=0
-6b(a-3b)=0
a-3b=0
a=3b
значит при любых значениях удовлетворяющих а=3b, исходное равенство будет верным