х²-12х+20= (х²- 2•х•6 +6²)+20 -6²=
= (х- 6)²+20-36= (х-6)² -16= (х-6)²- 4²=
(х-6+4)(х-6-4)=(х-2)(х-10)
Или:
х²-12х+20=0
D= b²- 4ac= 144-80=64 D>0,два корня.
х1,х2= - b ± √D/2a= 12± 8/2= 2 ; 10
x²-12x+20= (x -2)(x-10)
озьмём урожайность на первом участке за х,
а на втором тогда будет (х+5), т.к. на 5 больше.
Площадь первого возьмём за у,
тогда площадь второго будет (у-2), т.к. по условию на 2 меньше.
Получится система.
Урощайность на первом х, площадь первого у, собрали с первого всего 80
ху=80
Урожайность второго (х+5), площадь второго (у-2), всего со второго собрали 90, следовательно
(х+5)(у-2)=90
Остаётся решить данную систему уравнений
ху=80
ху=80 (1)
(х+5)(у-2)=90 (2) --> xy+5y-2x-10 = 90; 80+5y-2x-10 = 90; 5y - 2x = 20; y=4+0,4x
Из(1): х(4+0,4х) = 80; 0,4x2+4x - 80 = 0; x2 +10x -200=0; x=10, x=-20(не подходит)
Урожайность на первом участке 10 ц/га, а на втором : 10+5=15 ц/га.
ответ: 10 и 15.
1.В
Диагонали ромба не равны, они в точке пересечения делятся по полам.
2.
Зная что сумма внутренних углов четырехугольника 360° составим уровнение:
110+110+х+х=360
220+2х=360
2х=360-220
2х=140°
Х=70°
ответ:В
3.
S=a²
Увеличим в два раза:
S=(2a)²=4a²
ответ:Б, увеличится в 4 раза.
4.
Синус-отношение противолежайщего катета к гипотенузе.
По теореме Пифагора найдём гипотенузу:
5²+12²=25+144=169
√169=13
Синус равен-5/13
ответ:а
5.
Сначала найдём сумму внутренних углов в пятиугольнике:
180(n-2)=180(5-2)=180*3=540
Составим уровнение:
2х+4х+х+3х+8х=540
18х=540
Х=30
8*30=240°
ответ:В
6.
Найдем гипотенузу первого треугольника:
6²+8²=36+64=100
√100=10
Подобный ему треугольник в три раза больше него значит и катет будет в три раза больше:
6*3=18см
ответ:а
7.
Проведем две высоты и по теореме Пифагора найдём его:
10²-8²=100-64=36
√36=6
Найдем площадь трапеции:
S=Lh
L-средняя линия
h-высота
Найдем среднюю линию:
L=(4+20)÷2=24÷2=12
Подставляем:
S=12*6=72
ответ:72см²
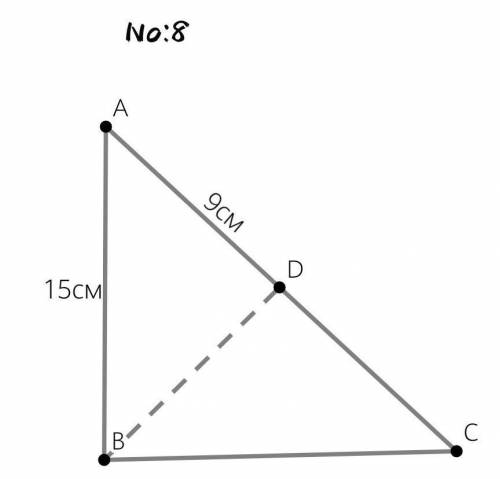
8.
15²=9*АС
225=9*АС
АС=25(гипотенуза)
По теореме Пифагора найдём катет:
25²-15²=625-225=400
√400=20
Найдем площадь:
S=1/2*15*20=150
ответ:150см²

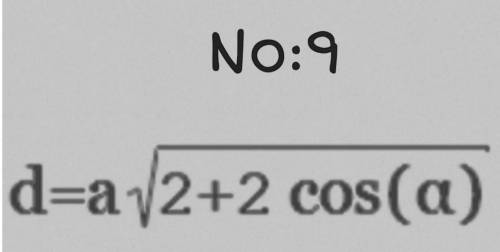
x² – 12x + 20 = (x – 2)(x – 10)
Объяснение:
x² – 12x + 20 = 0
D = 12² – 4·20 = 64 = 8²
x₁ = (12 – 8) / 2 = 2
x₂ = (12 + 8) / 2 = 10
x² – 12x + 20 = (x – 2)(x – 10)