Объяснение:
рассмотрим различные случаи когда b≠0 и b=0
1) b≠0
Ix-3I=(x+1)/b
x-3=±(x+1)/b это уравнение имеет два решения, это видно "невооруженным глазом" но на всякий случай найдем эти решения
а) x-3=(x+1)/b
х-3=bx+b
x-bx=3+b
x(1-b)=3+b
x₁=(3+b)/(1-b) первое решение
б) x-3=-(x+1)/b
х-3=-bx-b
x+bx=3-b
x(1+b)=3-b
x₂=(3-b)/(1+b) второе решение
2) b=0
x+1=0
x=-1 единственное решение
ответ при значении b=0 система имеет единственное решение
Примечание. в предыдущем решении получился такой же ответ но модератор его удалил с туманной формулировкой о несоответствии чего-то там чему-то там . посмотрим на этот раз удалит или нет
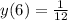
Объяснение:
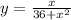
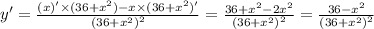
Для нахождения наибольшего значения функции нужно найти точку максимума,а для этого производную нужно приравнять к нулю
Т.к. знаменатель не может быть равен нулю => приравниваем к нулю числитель
36-х² = 0
х² = 36
х = ±6
Исследуем функцию
На промежутке х≤-6 производная отрицательная,значит функция убывает
На промежутке -6<х<6 производная положительная,значит функция возрастает
На промежутке,где х≥6 производная отрицательная,значит функция снова убывает
Из этого мы можем сделать вывод,что точкой максимума является х = 6 т.к. точка с возрастания переходит в убывание
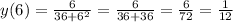
ответ: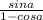 =
=
Умножим числитель и знаменатель на (1-cosa) , имеем:
=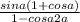 =
=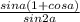 =
=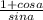
Объяснение: