В решении.
Объяснение:
Знайдіть усі точки графіка функції y=x2−5x+3 , у яких абсциса та ордината є протилежними числами.
Найдите все точки графика функции y=x² - 5x + 3 , в которых абсцисса и ордината являются противоположными числами.
Дана функция у = х² - 5х + 3.
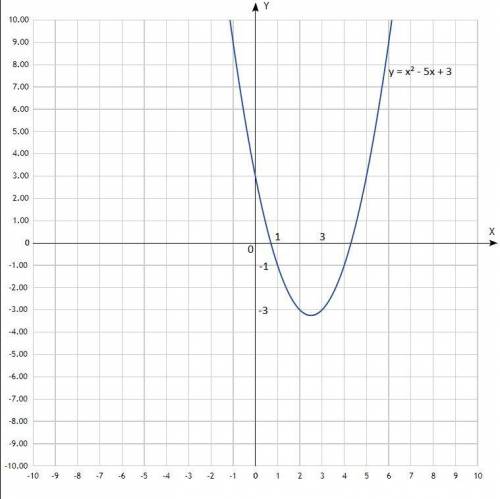
Построить график. График - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5 6 7 8
у 27 17 9 3 -1 -3 -3 -1 3 9 17 27
Согласно таблицы и графика существует две точки с указанными значениями х и у:
координаты: (1; -1); (3; -3).
объяснение:
выражение ( а - 6 ) * ( а + 2 ) - ( а + 5 ) * ( а - 7 ) и найдем значение выражения при а = - 6,5.
раскрываем скобки. для этого каждые значения в первой скобке, умножаем на каждое значение во второй скобке, и складываем их в соответствии с их знаками. тогда получаем:
( а - 6 ) * ( а + 2 ) - ( а + 5 ) * ( а - 7 ) = a ^ 2 + 2 * a - 6 * a - 6 * 2 - ( a ^ 2 - 7 * a + 5 * a - 5 * 7 ) = a ^ 2 + 2 * a - 6 * a - 12 - ( a ^ 2 - 7 * a + 5 * a - 35 ) = a ^ 2 - 4 * a - 12 - ( a ^ 2 - 2 * a - 35 ) = a ^ 2 - 4 * a - 12 - a ^ 2 + 2 * a + 35 = - 4 * a - 12 + 2 * a + 35 = - 2 * a + 23 = - 2 * ( - 6.5 ) + 23 = 13 + 23 = 36.