Обозначим cлагаемые за Х,У,Z
(X+Y+Z)/3>=1
Согласно неравенству о среднем арифметическом и среднем геометрическом достаточно доказать :
ХУZ>=1
Вернемся к исходным обозначениям
8abc>=(a+b)(b+c)(a+c)
Снова согласно неравенству о среднем арифметическом и среднем геометрическом видим
a+b>=2sqrt(ab) b+c>=2sqrt(сb) (a+c)>=2sqrt(ac)
поэтому можим заменить сомножители справа на произведение
2sqrt(ab)*2sqrt(aс)*2sqrt(сb)=8abc, что и доказывает неравенство.
Равенство достигается только при а=с=b
1)
ответ: В.
2)
ответ: А.
3)
ответ: Г.
4)
ответ: А.
5)
ответ: А.
6)
Для начала решим систему неравенств, определяющую область допустимых значений :
:
Возводим обе части уравнения в квадрат.
По теореме Виета:
3 не подходит под область допустимых значений.
ответ: корень только один, и он положительный.
7)
ответ:![(-9; -7]](/tpl/images/1579/1990/86283.png) .
.
8)
Областью определения функции является решение следующего неравенства:
Так как основание меньше единицы, то:
ответ:![(-\infty; 1,5]](/tpl/images/1579/1990/b9ec0.png) .
.
9)
Найдём область значения функции.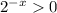 , тогда
, тогда 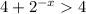 . Значит,
. Значит, 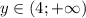 . Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).
. Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).
ответ: 5.
10)
Условие чётности функции: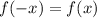 . Проверяем для каждой.
. Проверяем для каждой.
ответ: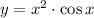 .
.