б) (x-y)+(x^2-y^2)=x-y+x^2-y^2=-(y-x)*(y+x+1)=(x-y)*(y+x+1)
д) (y-1)^2-(y^2-1)=y^2-2y+1-y^2+1=-2y+2=-2*(y-1)
∈ 
∞ 
∪ 
∞ 
∞ ∪ ∞ 
∈ 
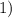
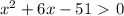
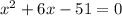
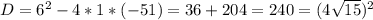
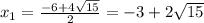
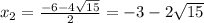
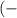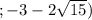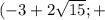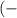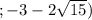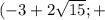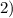
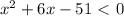
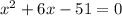
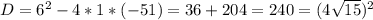
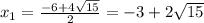
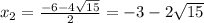
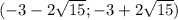
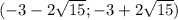
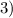
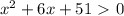
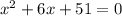
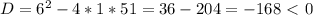
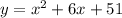
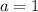положительный, то ветви параболы направлены вверх, а поскольку 
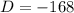отрицательный, то парабола не пересекается с осью 
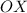. Поэтому парабола 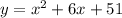расположена над осью 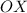; таким образом, при любом значении x имеем y>0. Значит, 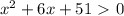при любом значении x. ∞ 
∞ 
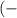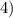
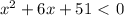
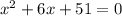
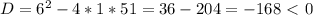
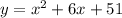
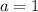положительный, то ветви параболы направлены вверх, а поскольку 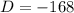отрицательный, то парабола не пересекается с осью 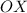. Поэтому парабола 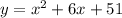расположена над осью 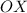; таким образом, при любом значении x имеем y>0. Значит, 
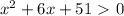при любом значении x. Следовательно, рассматриваемое неравенство не имеет решений. 
б) во второй скобке формула ---разность квадратов
... = (x-y) + (x-y)*(x+y) = (x-y)*(1+x+y)
д) во второй скобке формула ---разность квадратов
... = (y-1)*(y-1) - (y-1)*(y+1) = (y-1)*(y-1-y-1) = (y-1)*(-2) = -2*(y-1)