4+0+...4(2-n)=2n(3-n)
Док-во: 1) Проверим, что верно n=1: 4=2*1(3-1); 4=2(2); 4=4 -верно
2)Допустим, что верно для n=k, тогда: 4+...+4(2-k)=2k(3-k)
3)Докажем, что верно для n=k+1, тогда 4+...+4(2-(k+1))=2(k+1)(3-(k+1));
4+...+4(2-1-k)=2(k+1)(3-1-k); 4+...+4(1-k)=2(k+1)(2-k) -?
4+...+4(1-k)=2(k+1)(2-k)=> {4+...+4(2-k)}+4(1-k)= то, что находится в {...} заменяем на то, что получили во втором шаге, т.е. на 2k(3-k), получаем
= 2k(3-k)+4(1-k)=6k-2k^2+4-4k= 6k-4k-2k^2+4= 2k-2k^2+4= -(2k^2-2k-4)
Раскладываем квадратное уравнение -(2k^2-2k-4)=0; D=4+32=36=6^2
k1=(2-6)/4=-4/4=-1; k2=(2+6)/4=10/4 => -(2k^2-2k-4)=-2(k-10/4)(k+1)=(-2k+5)(k+1)=
=(5-2k)(k+1)=2(2.5-k)(k+1)
Получается, что неверно, но м.б. я гдн-то ошибся, но в общем такого вида получается док-во
у = х³ - 3х
у¹ = 3х² - 3
3х² - 3 = 0
х₁ = 1
х₂ = - 1
Это могут быть точки минимума и максимума функции.
Найдем значение производной на всех трех интервалах
х < -1 -1 < х < 1 и x > 1
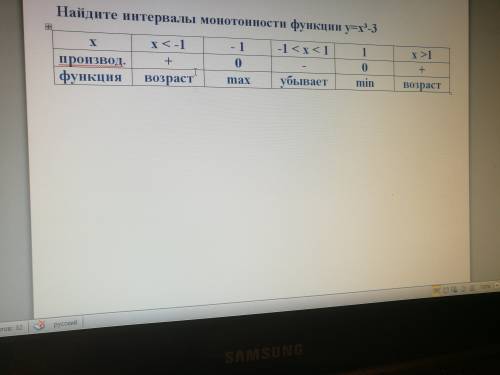
Внесем данные в таблицу (на фото).
Получим, на промежутке (-∞; -1) функция возрастает ,
На промежутке (- 1 ; 1) функция убывает
И на промежутке ( 1 ; + ∞) функция снова возрастает
в точке х= - 1 функция имеет максимум
в точке х = 1 функция имеет минимум.
Это и есть интервалы (или промежутки) монотонности функции
(b-4)²=b²-2×b×4+4²=b²-8b+16
(5a-10b)²=(5a)²-2×5a×10b+(10b)²=25a²-100ab+100b²
(3n³-4mn²)²=(3n³)²-2×3n³-4mn²+(4mn²)²=9n⁶-24mn⁵+16m²n⁴