найдем производную f´(x)=( x^4-2x^2-3)´=( x^4)´-2(x^2)´-(3)´=4х³-4х-0=4х³-4х=4х(х²-1)=4х(х-1)(х+1) найдем критические точки, т.е f´(x)=0 4х(х-1)(х+1)=0 х=0 или х=1 или х=-1 ++→х f´(-2)= 4*(--+1)= 4*(-)< 0 ( нас интересует знак, а не число) f´(-0,5)= 4*(-0,,5-,5+1)= 4*(-0,,5)*0,5> 0 f´(0,5)= 4*0,5*(0,5-1)(0,5+1)=4*0,5*(-0,5)*1,5< 0 f´(2)= 4*2*(2-1)(2+1)=4*2*1*3> 0 в точке х=-1 производная меняет знак с – на +, значит это точка минимума; в точке х=0 производная меняет знак с +на -, значит это точка максимума; в точке х=1 производная меняет знак с – на +, значит это точка минимума; 2) f(x)= x^2+3x /x+4 найдем производную f´(x)=( x^2+3x /x+4)´=( x^2+3x)´(х+4)- (x^2+3x)( x+4)´/ (x+4)² =(2х+3)(х+²+3х)*1/(х+4)²=(2х²+8х+3х+12-х²-3х)/(х+4)²=(х²+8х+12)/(х+4)²=(х+2)(х+6)/(х+4)² найдем критические точки, т.е f´(x)=0 (х²+8х+12)/(х+4)²=0 х²+8х+12=0 и х+4≠0; х≠-4 д=8²-4*1*12=64-48=16; х₁=-8+√16/2=-2; х₂=-8-√16/2=-6 т.е. (х²+8х+12)/(х+4)²=(х+2)(х+6)/(х+4)², т.к. (х+4)²> 0, нас интересует только знак, поэтому рассматриваем равносильное выражение (х+2)(х+6) ++→х f´(-7)= (-7++6)=-5*(-1)> 0 f´(-5)= (-5++6)=-3*1< 0 f´(-3)= (-3++6)=-1*3< 0 f´(0)= (0+2)(0+6)=2*6> 0 в точке х=-6 производная меняет знак с + на - значит это точка максимума; в точке х=-4 производная не меняет знак ,значит это точка не является точкой экстремума ; в точке х=-2 производная меняет знак с – на +, значит это точка минимума; удачи!
Объяснение:
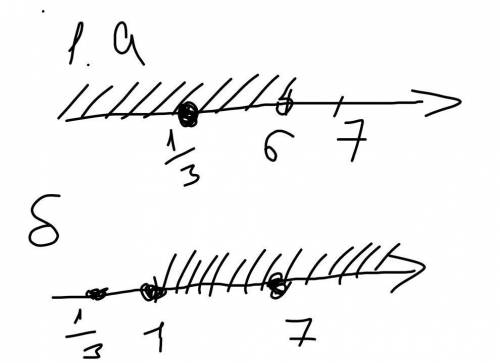
1. На фото 1
а) 1/3 є розв'язком, 7 - не є роза'язком
б) 7 є розв'язком, 1/3 не є розв'язком
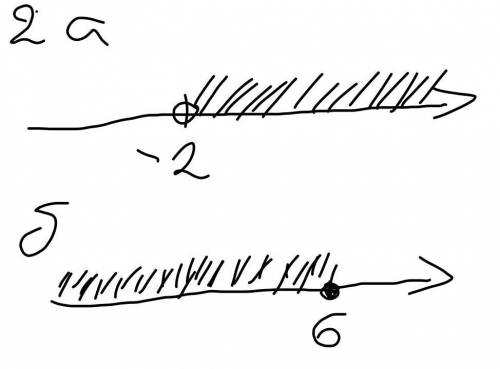
2. На фото 2
a) x∈(-2; +∞)
b) x(-∞; 6]
3. а) - 2
б) 9
4.
а) -4x≤ 16
x≥ 16/(-4)
x ≥ -4
x∈[-4; +∞)
б) 7-4x>6x-23
-4x-6x > -23-7
-10x > -30
x < -30/(-10)
x< 3
x∈(-∞; 3)
в) р-ня не має розв'язку, бо на нуль ділити не можна
г) 8x+(x-3)(x+3) ≥ (x+4)²
8x + x² - 9 ≥ x² + 8x +16
x² - x² + 8x - 8x ≥ 16 +9
0 ≥ 25
Р-ня не має коренів
e) домножимо обидві частини р-ня на 20:
5(5x-2) - 4(3-x) > 2(1-x)
25x - 10 -12 + 4x > 2- 2x
29x +2x > 2+12+10
31x > 24
x > 24/31
x ∈( 24/31; +∞)
Объяснение: