1) 8 < 2x+y < 30
2) 6 < xy < 48
3) -3 < x-y < 6
Объяснение:
3 < x < 8
2 < y < 6
1) 2x+y
сначала вычислим минимальный предел:
2*3+2=8;
затем максимальный:
8*3+6=30.
Получится 8 < 2x+y < 30
2) xy
сначала вычислим минимальный предел:
3*2=6;
затем максимальный:
8*6=48.
Получится 6 < xy < 48
3) x-y
Так как здесь присутствует вычитание. Сначала из меньшего значения x вычитаем большее значение y, так мы получим минимальный предел выражения x-y. Потом из большего значения x вычитаем меньшее значение y, так мы получим максимальный предел значения x-y.
сначала вычислим минимальный предел:
3-6=-3;
затем максимальный:
8-2=6.
Получится -3 < x-y < 6
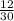*100% =0,4*100% = 40%
Объяснение:
X^2+2x-35=0
D=2*2-4*1*(-35)=4+140=√144=12
X1=-2+12/2=5. X2=-2-12/2=-14/2=-7
ответ х1=5
Х2=-7
Б)х^2+х-6=0
Д=1*1-4*1*(-6)=1+24=√25=5
Х1=-1-5/2*1=-3. Х2=-1+5/2*1=2
ответ х1=-3
Х2=2