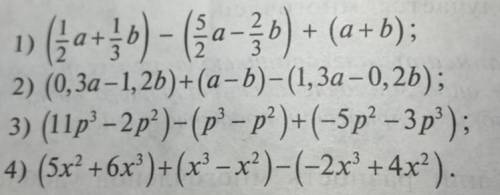


пара чисел (1;-6) для уравнения p^2*x+p*y+8=0
p^2 - 6p + 8 = 0
D = 36 - 4*8 = 36 - 32 = 4 = 2^2
p1 = (6-2)/2 = 2 p2 = (6+2)/2 = 4
p^2-6p+8=0
р*р - 4р - 2р + 2*4 = 0 (разложим на множители)
сгрупируем по парам - первые два(тут можно за скобки вынести "р")
и вторые сгрупируем - тут вынесим за скобки "-2" )
р * ( р - 4) - 2 (р - 4) = 0
теперь опять как бы вынесим за скобки (р-4)
(р-4) (р-2) = 0
р - 4 = 0 и р - 2 = 0
р = 4 р = 2
данная пара чисел (1;-6) будет являться решением уравнения p^2*x+p*y+8=0 при р = 2 или р = 4
Объяснение:
1) (1/2•(a) + 1/3•(b)) - (5/2•(a) - 2/3•(b)) +(a+b) = 1/2•(a) + 1/3•(b) - 5/2•(a) + 2/3•(b) + a+b= -2a+b+a+b= 2b-a
2) (0,3a - 1,2b)+(a-b) - (1,3a - 0,2b) = 0,3a - 1,2b + a - b - 1,3a+0,2b= -a +a -b-b= -2b
3) (11p³ - 2p²)-(p³-p²)+(-5p²-3p³) = 11p³- 2p² - p³+p²-5p²-3p³=7p³-6p²
4) (5x²+6x³)+(x³-x²)-(-2x³+4x²)= 5x²+6x³+x³-x²+2x³-4x²= 9x³