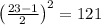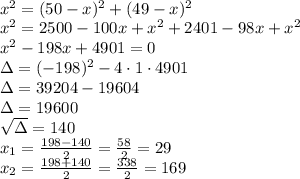
x^2=(50-x)^2+(49-x)^2
-2500+100x-2401+98x-x^2=0
-4901+198x-x^2=0
D=198^2-4*(-1)*(-4901)=39204-19604=19600
x1=(140-198)/(2*(-1))=29
x2=(-140-198)/(2*(-1))=169
Пояснение:
1) Если максимально просто объяснять, то когда одинаковые значения , а степени могут быть одинаковые или разные , умножаются , например как тут:
 *
* , то их степени суммируются , т.е.
, то их степени суммируются , т.е. 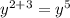
2) А при делении наоборот степени вычитаются, например :
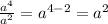 , т.е. от значения степени числителя
, т.е. от значения степени числителя 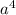 вычитаем значение знаменателя
вычитаем значение знаменателя 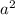 .
.
3) Есть ещё 1 пример, это когда имеется степень за скобкой, типа  , то тут степени умножаются друг на друга и у нас выйдет так:
, то тут степени умножаются друг на друга и у нас выйдет так:

Теперь решение:
Задача состоит в том, чтобы вместо точек подставить такое значение со степенью, чтобы получилось равенство.
1) - такие действия буду пропускать, как раз потренируешься.
- такие действия буду пропускать, как раз потренируешься.
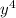 *
*  =
= 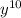 - для того, чтобы получить
- для того, чтобы получить 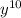 , нужно вместо точек вставить
, нужно вместо точек вставить  , тогда
, тогда  даст
даст  , и 4+6=10 =>
, и 4+6=10 =>  =
=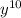
2)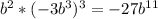
3)
4)
5)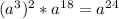
Если посмотришь на свойства степеней, то узнаешь ещё больше , чтобы быть всегда на готове.
Замечаем, что перестановки происходят отдельно среди четных чисел и среди нечетных чисел. Поэтому надо ответить на следующий вопрос: есть k предметов, расставленных в каком-то порядке слева-направо и соответствующим образом занумерованных; меняя местами за одну операцию два соседних предмета, нужно расставить их в том же порядке, но справа-налево. Говоря ученым языком, можно сказать, что сначала у нас не было ни одной инверсии (инверсия - это когда предмет с меньшим номером стоит правее предмета с большим номером), а надо сделать максимальное количество инверсий. Меняя местами соседей, мы каждый раз изменяем количество инверсий на 1. Конечно, нам невыгодно уменьшать количество инверсий, а выгодно - увеличивать. Но в каком порядке производить эту операцию - менять местами соседей - абсолютно непринципиально. Поступим, скажем, так. Поменяем сначала местами первый предмет и второй, затем первый и третий, первый и четвертый, и так далее, наконец, первый и последний. Всё. Первый предмет оказался на нужном месте и больше оттуда никуда сдвигаться не будет. Потребовалось нам для этого, естественно, (k-1) операция. Далее будем передвигать второй предмет до тех пор, пока он не поменяется местами с k-м предметом и не окажется рядом с первым, но левее первого. На это потребуется (k-2) операции. И так далее. Всего мы насчитаем  операций.
операций.
Остается подвести итоги. Окончательный ответ зависит от того, каково n - четное оно или нечетное.
1-й случай: n - четное, n=2m. Это означает, что у нас m четных чисел и m нечетных чисел. Всего операций получится
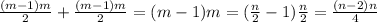
2-й случай. n - нечетное, n=2m+1. Это означает, что у нас m четных чисел и (m+1) нечетных чисел.Всего операций получится
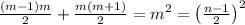
Решим задачу для n=5, 6, 7, 23.
n=5 - нечетное; 
n=6 - четное; 
n=7 - нечетное; 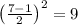
n=23 - нечетное;