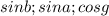
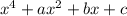по условию он должен быть, квадратом некого многочлена. 
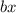, а он не возможен при квадрате , и заметим то что старшая степень равна 
. 
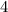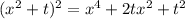. Что есть частный случаи многочлена.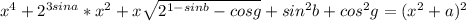 
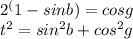
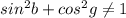так как оно противоречит условию 
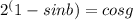что не имеет решений.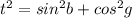 
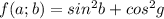очевидно 
. 
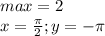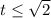. Что согласуется с значение 
. 
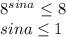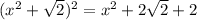
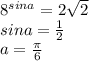
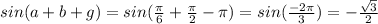
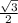
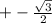
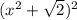
Это уравнение можно решить так:
x²=4
x=±2
x=-2
x=2