Объяснение:
1) прямая у=2x+37 не является касательной к графику функции f(x)=x³-3x²-7x+10 ни при каких значениях x. Докажем это. Предположим что это не так. пусть графики данных функций касаются в некоторой точке x₀=t. Тогда f(t)=t³-3t²-7t+10
f'(x)=3x²-6x-7; f'(t)=3t²-6t-7
Уравнение касательной будет иметь вид:
y=f(t)+f'(t)(x-t)=t³-3t²-7t+10+(3t²-6t-7)(x-t)=(3t²-6t-7)x-2t³+3t²+10=2x+37⇔
3t²-6t-7=2 и -2t³+3t²+10=37
3t²-6t-7=2
3t²-6t-9=0
t²-2t-3=0⇒t₁=-1, t₂=3
t=-1⇒-2t³+3t²+10=2+3+10=15≠37
t=3⇒-2t³+3t²+10=-16+27+10=21≠37
t∈∅
2) прямая у=x+1 касается к графику функции f(x)=ах²+2x+3
а≠0, иначе прямая касалась бы прямой.
Пусть графики данных функций касаются в некоторой точке x₀=t. Тогда f(t)=аt²+2t+3
f'(x)=2ax+2; f'(t)=2at+2
Уравнение касательной будет иметь вид:
y=f(t)+f'(t)(x-t)=аt²+2t+3+(2at+2)(x-t)=(2at+2)x-at²+3=x+1⇔2at+2=1 и -at²+3=1
2at+2=1⇒at=-0,5
2=at²=at·t=-0,5t⇒t=-4⇒a=1/8
3) x(t)=0,5t³-3t²+2t
v(t)=x'(t)=1,5t²-6t+2
v(6)=1,5·6²-6·6+2=54-36+2=20 м/с
Объяснение:
1) прямая у=2x+37 не является касательной к графику функции f(x)=x³-3x²-7x+10 ни при каких значениях x. Докажем это. Предположим что это не так. пусть графики данных функций касаются в некоторой точке x₀=t. Тогда f(t)=t³-3t²-7t+10
f'(x)=3x²-6x-7; f'(t)=3t²-6t-7
Уравнение касательной будет иметь вид:
y=f(t)+f'(t)(x-t)=t³-3t²-7t+10+(3t²-6t-7)(x-t)=(3t²-6t-7)x-2t³+3t²+10=2x+37⇔
3t²-6t-7=2 и -2t³+3t²+10=37
3t²-6t-7=2
3t²-6t-9=0
t²-2t-3=0⇒t₁=-1, t₂=3
t=-1⇒-2t³+3t²+10=2+3+10=15≠37
t=3⇒-2t³+3t²+10=-16+27+10=21≠37
t∈∅
2) прямая у=x+1 касается к графику функции f(x)=ах²+2x+3
а≠0, иначе прямая касалась бы прямой.
Пусть графики данных функций касаются в некоторой точке x₀=t. Тогда f(t)=аt²+2t+3
f'(x)=2ax+2; f'(t)=2at+2
Уравнение касательной будет иметь вид:
y=f(t)+f'(t)(x-t)=аt²+2t+3+(2at+2)(x-t)=(2at+2)x-at²+3=x+1⇔2at+2=1 и -at²+3=1
2at+2=1⇒at=-0,5
2=at²=at·t=-0,5t⇒t=-4⇒a=1/8
3) x(t)=0,5t³-3t²+2t
v(t)=x'(t)=1,5t²-6t+2
v(6)=1,5·6²-6·6+2=54-36+2=20 м/с
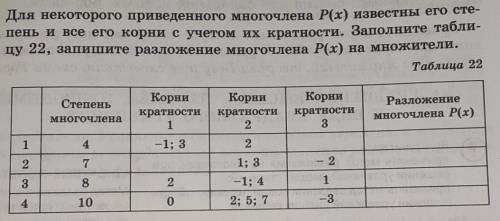
1.P(x) = (x + 1)(x - 3)(x - 2)²
2.P(x) = (x - 1)²(x - 3)²(x + 2)³
3.P(x) = (x - 2)(x + 1)²(x - 4)²(x - 1)³
4.P(x) = x(x - 2)²(x - 5)²(x - 7)²(x + 3)³