Пусть меньшая сторона — х метров, тогда большая — х+8 метров. Зная площадь площадки, составим и решим мат. модель:
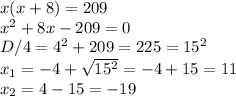
Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.
Следовательно, меньшая сторона — х = 11 метров;
большая — х+8 = 11+8 = 19 метров.
Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:
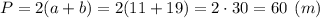
Необходимое количество упаковок равно:
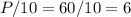
м.Большая сторона детской площадки равна: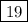 
м.Необходимое количество упаковок равно: 
.
Решение системы уравнений (-2; 3)
Объяснение:
Решить систему уравнений:
(2х+3у)/4 + (3х-2у)/5 = -23/20
(3х+4у)/2 - (5х-у)/3 = 22/3
Умножить первое уравнение на 20, второе на 6, чтобы избавиться от дроби:
5(2х+3у) + 4(3х-2у) = -23
3(3х+4у) - 2(5х-у) = 2*22
Раскрыть скобки:
10х+15у+12х-8у= -23
9х+12у-10х+2у=44
Привести подобные члены:
22х+7у= -23
-х+14у=44
Умножим первое уравнение на -2, чтобы решить систему методом сложения.
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
-44х-14у=46
-х+14у=44
Складываем уравнения:
-44х-х-14у+14у=46+44
-45х=90
х=90/-45
х= -2
Теперь подставляем значение х в любое из двух уравнений системы и вычисляем у:
-х+14у=44
14у=44+х
14у=44-2
14у=42
у=42/14
у=3
Решение системы уравнений (-2; 3)
в первом получится в числителе 2^-6 + 2^-6, складываем, получается 2^0 и делить на 8^-7
то есть ответ 8 в седьмой степени
во втором будет равно 5 ^ -2 то есть одна двадцать пятая