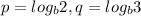и 
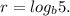Выразите число через p, q и r: 1) 
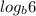; 2) 
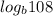; 3)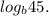 
Проще всего систему решить так
x+y=7
x^2-2xy+y^2=9
x+y =7
(x-y)^2 = 9 то есть наша система разбивается на 2 примитивных
x+y = 7 x+y = 7
x-y = 3 x-y = -3
2x = 10 2x=4
x=5 x=2
y=7-x=7-5=2 y=7-x=7-2=5
ответ x1=5 x2=2
y1=2 y2=5
Обрати внимание, что решения симметричные, это было понятно с самого начала, так как сама система(уравнения системы) симметричные, поэтому можно было сначала доказать лемму
Если (x0,y0) решение, то и (y0,x0) тоже решение
После чего найти только ОДНО решение, второе получается автоматически.
Этот метод часто применяется в сложных системах, где сложно получается решение, чтобы не проводить лишних расчётов.
В нашем случае всё просто, но этот метод(подход) нужно всегда иметь в виду.
а+д = 10-
ад=7 Решаем подстановкой: д = 10-а
а(10 - а) = 7
10а -а² = 7
а² -10а +7 = 0
а = 5+-√(25 - 7)= 5+-√18= 5+-3√2
Здесь 2 решения:
1) а = 5+3√2 2) а = 5-3√2
д=10 -5 - 3√2= 5 - 3√2 д=10 - 5 + 3√2 = 5 +3√2
Наша прогрессия: Наша прогрессия:
5+3√2; б; с ;5-3√ 2 5-3√2; б; с; 5 + 3√2
б² = с(5 +3√2)
с² = б(5-3√2)
б² / с² = с(5 +3√2)/ б(5-3√2)
б³(5-3√2) = с³(5+3√2)
б³/с³ = (5+3√2)/(5-3√2)