Дана функція:
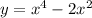
Знайдемо її похідну ( y' = g(x) ):
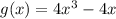
Знайдемо значення похідної в 0 (g(x) = 0):
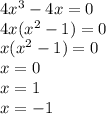
Ми знайшли 3 можливі точки екстремуму: 0, 1, -1. Перевіримо, чи дійсно ці точки є екстремумами функції:
1) Підставимо в похідну точку -2. Значення від'ємне, отже функція спадає;
2) Підставимо в похідну точку -0.5. Значення додатне, отже функція зростає;
3) Підставимо в похідну точку 0.5. Значення від'ємне, отже функція спадає;
4) Підставимо в похідну точку 2. Значення додатне, отже функція зростає.
Отже на проміжку xє(-∞;-1) функція спадає; хє(-1;0) – функція зростає; хє(0;1) – функція спадає; хє(1;+∞) – функція зростає. Отже ці точки дійсно є екстремумами функції.
Відповідь: -1, 0, 1.
Объяснение:
Panzerkampfwagen VIII «Maus» (Maus — «Мышь», иное название — Porsche Typ 205 или Pzkpfw.VIII Maus) — сверхтяжёлый танк, спроектированный в Третьем рейхе в период с 1942 по 1945 годы под руководством Фердинанда Порше. Является самым крупным по массе танком из всех, когда-либо воплощённых в металле (боевая масса — 182 тонны). Было построено всего два экземпляра машины. В боевых действиях не участвовали. На данный момент в мире сохранился только один танк «Маус», собранный из частей обоих экземпляров, в Бронетанковом музее в Кубинке[5