(см. объяснение)
Объяснение:
Рассмотрим уравнение:
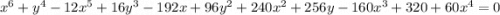
Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что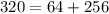 
.
Учитывая это перепишем уравнение:
Теперь выполним хитрое преобразование:
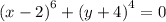
Обращаем внимание на то, что равенство верно только, если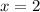 
, а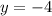 
.
Тогда решением исходного уравнения является пара чисел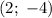 
.
Уравнение решено!
У меня нету книги Ты толжет поставить фотографии .очень бы хотела