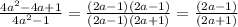1) y^4-81=(y-3)*(y+3)*(y^2+9)
2) (х-2)(2х+6)=0
2x^2+2x-12=0
D=2^2-4*2*(-12)=4+96=100
x1=(10-2)/(2*2)=8/4=2
x2=(-10-2)/(2*2)=-12/4=-3
3) x^3-9x=0
(x-3)*x*(x+3)=0
x-3=0
x=3
x=0
x+3=x
x=-3
4) (4а^2-4a+1)/(4a^2-1)=(2a-1)/(2a+1)
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом[1].
Вектор с началом в точке {\displaystyle A}A и концом в точке {\displaystyle B}B принято обозначать как {\displaystyle {\overrightarrow {AB}}}\overrightarrow {AB}. Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например {\displaystyle {\vec {a}}}{\vec {a}}. Другой рас записи: написание символа вектора прямым жирным шрифтом: {\displaystyle \mathbf {a} }{\mathbf {a}}.
1)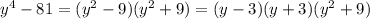
2)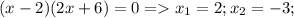
3)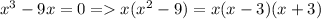
4)