Что бы построить график данной функции, исследуем данную функцию:
1. Область определения: Так как данная функция имеет смысл при любом х. То:
2. Область значения: Так как данная функция - квадратичная, а так же, главный коэффициент а положителен.То, график данной функции - парабола и ее ветви направлены вверх.
Следовательно, область значения данной квадратичной функции находится следующим образом (при а>0): - где D дискриминант.
Найдем дискриминант:
Теперь находим саму область:
3. Нули функции: Всё что требуется , это решить уравнение.
Следовательно, функция равна нулю в следующих точках:
4. Зная нули функции, найдем промежутки положительных и отрицательных значений. Чертим координатную прямую, на ней отмечаем корни уравнения, записываем 3 получившийся промежутка и находим на данных промежутках знак функции:
То есть:
5. Промежутки возрастания и убывания. Для этого найдем вершину параболы:
Промежуток убывания:
Промежуток возрастания:
Если вы изучали понятие экстремума, то: --------------------------------------------------------------- 6. Экстремум функции. Так как а>0 и функция квадратичная. То вершина является минимумом данной функции. Следовательно: --------------------------------------------------------------- 7. Ось симметрии
Зная вершину, имеем следующее уравнение оси симметрии:
Основываясь на данных, строим график данной функции. (во вложении).
Воспользуемся формулой для поиска корней уравнения:
ax^2+bx+c=0
x1=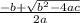
x2=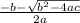
Пойдем от противного и приравняем корни х1 и х2:
(6+ )\2a=(6-
)\2a=(6- )\2a
)\2a
Сократим:
(6+ )=(6-
)=(6- )
)
Они могут быть равны только при обоих частях равных 0, соответственно нужно:
36-4а^2=0
a^2=9
a1=3
a2=-3
Но корень не может быть отрицательным, соответственно есть ограничение:
36-4а^2>0
соответственно а должно лежать в интервале (-3,3)
ответ:уравнение будет иметь разные корни при а=(-3,3)