
![\int \dfrac{x\, dx}{\sqrt[4]{(16+x^2)^5}}=\Big[\ t=16+x^2\ ,\ dt=2x\, dx\ ,\ x\, dx=\dfrac{dt}{2}=\ \Big]=\\\\\\=\dfrac{1}{2}\int \dfrac{dt}{t^{5/4}}=\dfrac{1}{2}\cdot \dfrac{t^{-1/4}}{-1/4}+C=-2\cdot \dfrac{1}{\sqrt[4]{16+x^2}}+C](/tpl/images/1644/8451/04c16.png)
![\int\limits^{\infty }_0\dfrac{x\, dx}{\sqrt[4]{(16+x^2)^5}}=\lim\limits _{A \to +\infty}\int\limits^{A}_ {0}\dfrac{x\, dx}{\sqrt[4]{(16+x^2)^5}}=\lim\limits _{A \to +\infty}\, \dfrac{-2}{\sqrt[4]{16+x^2}}\, \Big|_0^{A}=\\\\\\=\lim\limits _{A \to +\infty}\, \Big(\dfrac{-2}{\sqrt[4]{16+A^2}}+\dfrac{2}{\sqrt[4]{16^5}}\Big)=\Big[\ \dfrac{-2}{+\infty }+\dfrac{2}{2^5}=-0+\dfrac{2}{32}\ \Big]=\dfrac{1}{16}\ ,\ sxoditsya](/tpl/images/1644/8451/c8ce1.png)
В решении.
Объяснение:
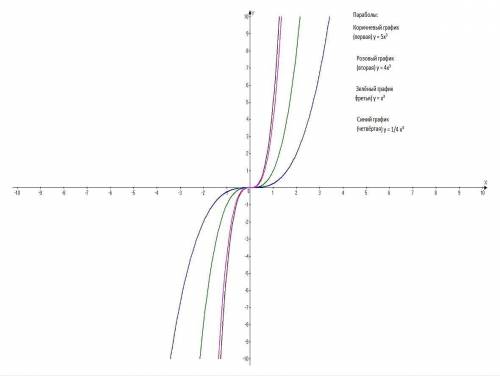
Построить в одной системе координат графики функций:
у = х³; у = 5х³; у = х³/4; у = 4х³.
Все графики - кубические параболы с вершиной в начале координат (0; 0). у = х³ - классическая парабола, остальные, в зависимости от коэффициента перед х³ "уже" или "шире" её.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
1) у = х³;
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
2) у = 5х³;
Таблица:
х -2 -1 0 1 2
у -40 -5 0 5 40
3) у = 1/4 х³ = х³/4;
Таблица:
х -3 -2 -1 0 1 2 3
у -6,75 -2 -0,25 0 0,25 2 6,75
4) у = 4х³;
Таблица:
х -2 -1 0 1 2
у -32 -4 0 4 32
в первом ящике х яблок, во втором у.
забираем из первого половину. там остается х-1/2х=1/2х яблок.
из второго забираем треть. там остается у-1/3у=2/3у.
теперь яблок в ящиках поровну, т.е. 1/2х=2/3у
а общее кол-во яблок в ящиках уменьшилось на 150, т.е. 1/2х+1/3у=150.
решаем систему
1/2х=2/3у
1/2х+1/3у=150
из первого уравнения у=1/2х:2/3=1/2х*3/2=3/4х
подставляем значение у во второе уравнение
1/2х+1/3*3/4х=150
1/2х+1/4х=150
3/4х=150
х=150:3/4=150*4/3=200
тогда у=3/4*200=150
первоначально в ящиках было 200+150=350 яблок.