Число р при делении на 3 может давать остатки 0,1 или 2.
Если число р при делении на 3 дает остаток 1, то оно имеет вид
p=3k+1, где k - некоторое целое число
Но тогда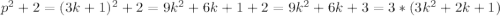 
, а значит число 
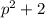не является простым. Значит такой случай невозможен
Если число р при делении на 3 дает остаток 2, то оно имеет вид
p=3k+2, где k - некоторое целое число
Но тогда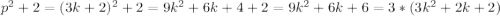 
, а значит число 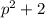не является простым. Значит такой случай невозможен
Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.
При р=3: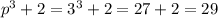 
- простое, что и требовалось доказать.Доказано
6 превратить в произведение
Cos9x – cos13x – sin2x = ( Cos9x – cos13x ) – sin2x =
= - 2*sin [(9x+13x)/2]* sin [(9x-13x)/2] - sin2x =
= -2*sin11x *sin(-2x) - sin2x = 2*sin11x * -sin(-2x) - sin2x = **-sin(-2x)=sin2x
= 2*sin11x * sin2x - sin2x = sin2x * (2*sin11x - 1)
7 Сократите
(Cos9a +cos7a ) / (cos6a*cos2a – sin6a*sin2a)
Преобразуем по частям
Числитель - переход от суммы к произведению
Cos9a +cos7a = 2*cos[(9a+7a)/2 ]* cos[(9a-7a)/2 ]=2*cos8a*cosa (1)
Знаменатель - формула сложения
cos6a*cos2a – sin6a*sin2a=cos (6a +2a) =cos 8a (2)
подставим части в дробь
(1) / (2) = 2*cos8a*cosa / cos 8a = 2 cos a
8 доказать тождество
2/ (1-sin2a) =1+ctg2 (a –п/4)
Преобразуем по частям
Левая часть
2/ (1-sin2a) = 2/ (1-2sinα*cosα)= 2/ (sin2α +cos2α -2sinα*cosα)=2/( sinα-cosα)2
Правая часть
1+ctg2 (a –п/4)=1/sin2(a-п/4)=1/(sina*cos п/4 –sin п/4*cosa)2=
=1/ (sina * 2/√2 - 2/√2 *cosa)2 =1/ (4/2 *( sinα-cosα)2) =2/( sinα-cosα)2
2/( sinα-cosα)2 =2/( sinα-cosα)2
В обеих частях одно и то же выражение
Доказано
-х(х+2)+(х-5)^2= -х^2-2х+х^2-10х+25= -12х+25=
-12×(-3/8)+25=9/2+25=59/2= 29 1/2