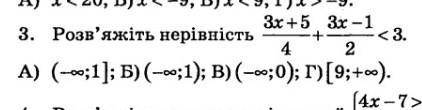
Упрощение
(4x 2 + -9) + -2 (2x + -3) + x (2x + -3) = 0
Измените порядок условий:
(-9 + 4x 2 ) + -2 (2x + -3) + x (2x + -3) = 0
Избавиться от скобок, заключающих (-9 + 4x 2 )
-9 + 4x 2 + -2 (2x + -3) + x (2x + -3) = 0
Измените порядок условий:
-9 + 4x 2 + -2 (-3 + 2x) + x (2x + -3) = 0
-9 + 4x 2 + (-3 * -2 + 2x * -2) + x (2x + -3) = 0
-9 + 4x 2 + (6 + -4x) + x (2x + -3) = 0
Измените порядок условий:
-9 + 4x 2 + 6 + -4x + x (-3 + 2x) = 0
-9 + 4x 2 + 6 + -4x + (-3 * x + 2x * x) = 0
-9 + 4x 2 + 6 + -4x + (-3x + 2x 2 ) = 0
Измените порядок условий:
-9 + 6 + -4x + -3x + 4x 2 + 2x 2 = 0
Объедините похожие термины: -9 + 6 = -3
-3 + -4x + -3x + 4x 2 + 2x 2 = 0
Объедините похожие термины: -4x + -3x = -7x
-3 + -7x + 4x 2 + 2x 2 = 0
Зерноуборочный подобные термины: 4x 2 + 2x 2 = 6x 2
-3 + -7x + 6x 2 = 0
Решение
-3 + -7x + 6x 2 = 0
Решение для переменной 'x'.
Разложите на множители трехчлен.
(-1 + -3x) (3 + -2x) = 0
Подзадача 1
Установите коэффициент '(-1 + -3x)' равным нулю и попытайтесь решить:
Упрощение
-1 + -3x = 0
Решение
-1 + -3x = 0
Переместите все термины, содержащие x, влево, все остальные термины - вправо.
Добавьте «1» к каждой стороне уравнения.
-1 + 1 + -3x = 0 + 1
Объедините похожие термины: -1 + 1 = 0
0 + -3x = 0 + 1
-3x = 0 + 1
Объедините похожие термины: 0 + 1 = 1
-3x = 1
Разделите каждую сторону на «-3».
х = -0,3333333333
Упрощение
х = -0,3333333333
Подзадача 2
Установите множитель '(3 + -2x)' равным нулю и попытайтесь решить:
Упрощение
3 + -2x = 0
Решение
3 + -2x = 0
Переместите все термины, содержащие x, влево, все остальные термины - вправо.
Добавьте «-3» к каждой стороне уравнения.
3 + -3 + -2x = 0 + -3
Объедините похожие термины: 3 + -3 = 0
0 + -2x = 0 + -3
-2x = 0 + -3
Объедините похожие термины: 0 + -3 = -3
-2x = -3
Разделите каждую сторону на «-2».
х = 1,5
Упрощение
х = 1,5
Решение
х = {-0,3333333333, 1,5}
n=6
Объяснение:
известно, что формула перестановок :
Pn=n!, где n - количество элементов, участвующих в перестановках
при этом n!=1*2*...*(n-1)*n,
и 0!=1, 1!=1, 2!=1*2=2, 3!=1*2*3=6 и т.д.
Соответственно, в данной задаче Pn<724, требуется найти n max?
Отметим, что n - не отрицательное число,
то есть n≥0
Рассмотрим возможные варианты:
n=0, 0!=1
n=1, 1!=1
n=2, 2!=1*2=2
n=3, 3!=1*2*3=2*3=6
n=4, 4!=1*2*3*4=6*4=24
n=5, 5!=1*2*3*4*5=24*5=120
n=6, 6!=1*2*3*4*5*6=120*6=720
n=7, 7!=1*2*3*4*5*6*7=720*7=5040 > 724 - не подходит,
Следовательно, подходящее к условии задачи число n имеет следующее условие:
0≤n≤6, то есть n max = 6
Объяснение:
(3x+5)/4 + (3x-1)/2 < 3 // * 4
3x+5+6x-2 < 12
9x < 9 // : 9
X<1
(1) >
X ∈ (-∞ ; 1)
OTBET: Б