Да
Пошаговое объяснение:
Сначала докажем иррациональность числа √2.
Пойдем от противного. Пусть число √2 рационально. Тогда ∃ m, n ∈ Z\{0} такие, что √2=m/n. Тогда:
2=m²/n² ⇒ 2n²=m²
Квадрат любого целого числа содержит в своем разложении на простые множители четное кол-во двоек. Тогда m² и n² делятся нацело на четное кол-во двоек. Тогда 2n² делится на нечетное кол-во двоек.
Получили, что ненулевые целые числа справа и слева от знака равенства нацело делятся на разное кол-во двоек. Противоречие.
Значит наше предположение неверно, и число √2 иррационально.
Тогда и число -√2 тоже иррационально.
Их сумма равна √2+(-√2)=√2-√2=0 - рациональное число.
Значит при сложении иррациональных чисел может получиться рациональное число.
Можно решить графическим
x^2+y^2=R^2 (уравнение
окружности с радиусом R и центром в начале координат)
1)Построим грвфик первого уравнения
x^2+y^2=3^2
Координаты центра окружности(0;0);Радиус R=3
2)Построим график второго уравнения
y-x^2=p
y=x^2+p (парабола, ветви вверх, координаты вершины(0;p))
Если p увеличивается, то парабола смещается вверх вдоль оси y и наоборот, если p уменьшается
3) Мы имееем:
- окружность с R=3 с центром в начале координат
- параболу, которая двигается только вдоль оси y, ветви вверх
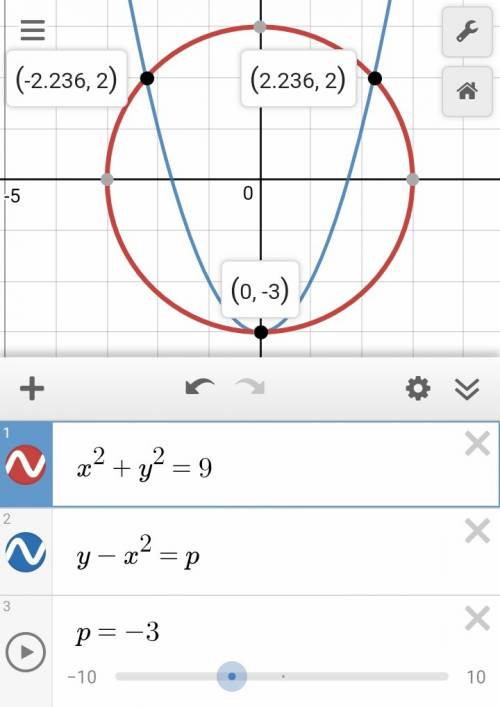
Мы уже имеем 2 решения благодаря ветвям параболы, которые пересекают окружность в 2-ух точках. Как получить третью точку пересечения(т.е третье решение)? Сместим параболу так, чтобы ее вершина касалась окружности И ветви также продолжали пересекать окружность в 2 точках
Сместим с параболу на -3, т.е вниз на 3 точки(3 потому что радиус окружности также равен 3)
Получим конечный результат(см рис.). 3 решения при p=-3
ответ: p=-3
Пусть х собственная скорость, тогда (х+2) км/ч скорость по течению реки, а (х-2) км/ч скорость против течения
45/(х+2)+45/(х-2)=14
45х-90+45х+90=14х²-56
90х=14х²-56
14х²-90х-56=0
D=2025-4*7*(-28)=2809
х=(45+53)/14=7 км/ч собственная скорость спортивной лодки