1. Целыми выражениями называются: а) все числовые выражения; б) выражения с переменными, содержащие операции сложения, вычитания, умножения и возведения переменных в натуральную степень.
Примеры целых выражений:
Выражения не являются целыми, так как они содержат операции возведения в целую отрицательную степень и деления на переменную.
2. Одночлены и многочлены являются целыми выражениями.
3. Если в выражении с переменными, кроме операций сложения, умножения, вычитания и возведения в натуральную степень, производится и операция деления на переменную, то такие выражения называются дробными выражениями.
Например, — дробные выражения.
Надо взять такие числа, которые будут максимально равны между собой и при этом будут являться целыми.
Эти числа 9 и 9.
Проверим по квадратам:
81 + 81 = 162
Теперь проверим другие числа. Один множитель уменьшим на единицу, а другой увеличим на единицу:
64 + 100 = 164
Как видим сумма получилась больше предыдущей. Возьмём еще:
9 + 729 = 738
Значительно больше первой суммы. Вывод:
надо уравнять множители, чтобы получить наименьшую сумму квадратов этих множителей.
ответ: 81 = 9 * 9, т.к.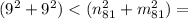
162 < суммы квадратов множителей (при "n" </> 9, "m" </> 9).
*n81^2 - квадрат множителя 81.