Медиана выборки 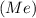 — это число, делящее пополам упорядоченную совокупность всех значений выборки по количеству, то есть половина значений выборки не большие за медиану, а половина — не меньшие. Если количество элементов нечетное (
— это число, делящее пополам упорядоченную совокупность всех значений выборки по количеству, то есть половина значений выборки не большие за медиану, а половина — не меньшие. Если количество элементов нечетное (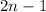 ), то медианой является «среднее» число в упорядоченном их наборе, а если количество элементов четное (
), то медианой является «среднее» число в упорядоченном их наборе, а если количество элементов четное (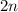 ), то — среднее арифметическое двух «средних»чисел в этом наборе.
), то — среднее арифметическое двух «средних»чисел в этом наборе.
Например, для упорядоченной выборки, состоящей из нечетного количества элементов 3, 6, 8, 11, 19, 24, 33, медианой будет число, стоящее по середине вариационного ряда.
Например, для упорядоченной выборки, состоящей из четного количества элементов 1, 4, 4, 7, 8, 15, 24, 24, «серединой» выборки является сразу два числа: 7 и 8. Считают, что медиана такой выборки равна их среднему арифметическому: 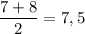 .
.
x=1
Объяснение:
рассмотрим функцию:
![f(x)=\frac{x^2}{4}+\frac{3}{4} -\sqrt[4]{2x-1}](/tpl/images/1359/7990/11395.png)
2x-1≥0 ⇔ x≥0.5
Её область определения: D(f)=[0.5;+∞)
Исследуем ее с производной:
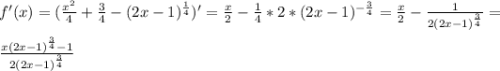
Находим нули числителя:
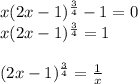
Замечаем, что слева стоит возрастающая функция, справа - убывающая. Поэтому если и есть корень, то он единственный!
Не трудно догадаться, что корнем будет x=1
Теперь находим нули знаменателя:
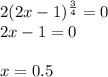
метод интервалов с учетом D(f)
(0,5)---[1]---->ₓ
С пробных точек узнаем знаки промежутков и получаем:
(0,5)---[1]+++>ₓ
На интервале (0,5;1) производная отрицательна, значит функция убывает.
На интервале (1;+∞) производная положительна, значит функция возрастает
Таким образом x=1 - точка минимума и в том числе точка наименьшего значения функции
![f(1)=\frac{1}{4}+\frac{3}{4}-\sqrt[4]{2*1-1}=0](/tpl/images/1359/7990/52c95.png)
f(1)=0 - минимум и наименьшее значение функции
Таким образом мы выяснили, что f(x)≥0 при всех допустимых x, а равенство f(x)=0 достигается только в точке x=1 (в точке минимума)
204542457542421575/3452642